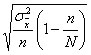16.Сред. И предел. Ошибки выборки. Взаимосвязь показ-лей ошибки выборки с объемом выб. Совок-ти и способом отбора.
Осн. преимущ-во выбороч. наблюд-я— возм-ть рассчитать случайную ошибку выборки.
Ошибки выборки бывают систематич. и случайные.
Сист —когда нарушен осн. принцип выборки — случайности.
Случ — т.к. структура выбороч. совок-ти всегда отличается от структуры ген. совок-ти, т.е. все же имеются расхождения между хар-ками выбор. и ген. совок-ти. Случайные ошибки выборки делятся на средние и предельные.
Чаще всего рассчит. ошибку средней и ошибку доли. Исп-ся усл. обознач-я:
-
— ср, рассчит. в пределах ген совок-ти;
— ср, рассчит в пределах выб совок-ти;
p
— доля данной группы в ген совок-ти;
w
— доля данной группы в выб совок-ти.
Используя условные обозначения, ошибки выборки для средней и для доли можно записать следующим образом:
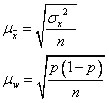
На практике дисперсию признака(неизвест. хар-ку ген совок-ти) заменяют аналогич. хар-ками выб. совок-ти.
Формулы опред-я ср. ошибки для различ. способов отбора:
|
Повторный |
Бесповторный |
||
Способ отбора |
ошибка средней |
ошибка доли |
ошибка средней |
ошибка доли |
Собственно-случайный и механический |
|
|
|
|
Типический |
|
|
|
|
Серийный |
|
|
|
|
-
— предельная ошибка;
— средняя ошибка;
N
— численность выборки;
N
— численность генеральной совокупности;
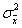
— общая дисперсия;
W
— доля данной категории в общей численности выборки;
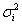
— средняя из внутригрупповых дисперсий;
2
— межгрупповая дисперсия;
R
— число серий в выборке;
R
— общее число серий.
Предел. ошибка (максимал возмож. расхожд. средних или максимум ошибок при заданной вер-ти ее появления) связана со ср. ошибкой выборки:
= t,,
где t — коэфф. доверия, функц-но связ. с вер-тью предел. ошибки. В завис-ти от вер-ти коэфф. доверия t принимает след. Знач-я:
t |
1 |
1,5 |
2 |
2,5 |
3 |
4 |
P |
0,683 |
0,866 |
0,954 |
0,988 |
0,997 |
0,9999 |
Т.о., величина предел. ошибки зависит от:
колеблемости признака (прямая связь), кот. харак-зует величина дисперсии;
числ-ти выборки (обратная связь);
доверительной вер-ти (прямая связь);
метода отбора.
Формула предел. ошибки позволяет решать задачи:
опред. величины ошибки, а также 1) опред. необход. числ-ть выборки, при кот. пределы возмож. ошибки не превышают некот. заданной величины. 2) определить вер-ть, что в выборке ошибка будет заключаться в заданных пределах.
Необход. числ-ть выборки
для повтор. отбора:
|
при бесповтор.:
|
17. Задачи стат-ки в изуч-и взаимосвязей общест. явл-й, виды и формы связей.
Задачи стат. изуч.я взаимосвязей:
-Установл-е наличия направ-я связи;
-кол-венное измер-е влияния факторов;
-измер-е тесноты связи;
-оценка достовер-ти получ. данных.
Качественный анализ изучаемого явления позволяет выделить основные причинно-следственные связи данного явления, установить факторные и результативные признаки.
Взаимосвязи, изучаемые в статистике, могут быть классифицированы по ряду признаков:
1)По характеру завис-ти: функциональные (жесткие), корреляционные (вероятностные).
Функцион. связи –каждому знач-ю факторного признака соответ-ет единств. знач-е результатив. признака.
При коррел-х связях отдел. знач-ю фактор. признака могут соответ-ть разные знач-я результ. признака.
Такие связи проявл-ся при большом кол-ве наблюд-й, ч-з изменение ср. величины результ. пр-ка под воздействием фактор. пр-ков.
2) По аналитич-у выражению: прямолинейные, криволинейные.
3) По напр-ю: прямые, обратные.
4) По числу факт. пр-ков, к. оказывают влияние на резул. пр-к: однофакт-е, многофакт-е.
18. Методы оценки взаимосвязей атрибутивных признаков. Коэффициенты ранговой корреляции.
Методы оценки тесноты связи распределяются на параметрические (корреляционные) и непараметрические. Параметрические методы основаны на использовании оценок параметров распределения вероятностей изучаемых величин: математического ожидания, дисперсии и т.д.
Непараметрические методы применяют для оценки связи атрибутивных (качественных) признаков и для оценки корреляционных связей.
Атрибутив.признак – качественный(напр., национальность, пол),т.е. можно измерить только кол-во объектов, имеющих этот признак, а не кол-во самого признака.
Важное место в статистическом изучении взаимосвязей занимают следующие методы:
1. Метод приведения параллельных данных.
2. Метод аналитических группировок.
3. Графический метод.
4. Балансовый метод.
5. Индексный метод.
6. Корреляционно-регрессионный.
Ранг – порядковый номер признака, упорядоч-го по возраст-ю/убыв-ю ряда значений.
Коэф.
ранговой корр-ции Спирмена 
,
где d
– разность рангов 2х рядов чисел (ri-si),
n-число
наблюдений.
Коэф ранговой корр-ции Кендала Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент корреляции Кендалла:
,
где 
—
суммар.число
наблюд-й, следующих за текущими наблюд-ми
с бОльшим значением
рангов Y.
—
||-||
с меньшим значением
рангов Y. (равные
ранги не учитываются!). P
и
Q
считаются по всем членам ряда.
19. Понятие о корреляционно-регрессионном анализе.
Связь как синхронность (согласованность) – корреляционный анализ.
Связь как зависимость (влияние) – регрессионный анализ (причинно-следственные связи).
В регрессионном анализе один из признаков зависит от другого.
• Первый признак, кот. влияет на второй, назыв. факторным (независ.). второй(зависимый) - результатив. Не всегда можно однозначно опред-ть, какой из признаков независ., а какой – завис. Тогда связь двунаправленная.
ОТЛИЧИЯ
Коэф. коррел-и
• Принимает значения от -1 до +1,
• Безразмерная величина,
• Показывает силу связи м-у признаками,
• Знак коэф говорит о направлении связи(- обратная, +прямая).
Коэф. регрес.
• Может принимать любые значения,
• Привязан к единицам измерения обоих признаков,
• Показывает структуру связи м-у признаками,
• Знак коэф-а говорит о напр-и связи
Для оценки силы связи в теории корреляции применяется шкала английского статистика Чеддока: слабая — от 0,1 до 0,3; умеренная — от 0,3 до 0,5; заметная — от 0,5 до 0,7; высокая — от 0,7 до 0,9; весьма высокая (сильная) — от 0,9 до 1,0.
20.Ряды динамики, их элементы и правила построения. Виды рядов динамики.
Всякий ряд динамики состоит из двух элементов:
время (t) — это либо момент времени (дата), либо промежуток времени, к кот. относится стат. пок-ль; и уровень ряда (y) — сам стат. пок-ль, кот. рассчит-ся за ряд интервалов.
ВИДЫ по трем признакам:
1. По времени:
моментные дин. ряды; и интервальные дин. ряды.
Момен. ряд —если пок-ль опред-ся на дату, момент времени. Напр: числ-ть насел-я на нач. года.
Интер. - если пок-ль это результат за интервал (период) времени. Напр: производство ВВП за год, выпуск продукции за месяц.
Уровни интервал. дин.ряда могут суммир-ся между собой. Суммир-е уровней момен. ряда не имеет смысла.
В осн. ч-з момен. ряды предст-ся стат. пок-ли (признаки), через интерв — динамич.
2.По полноте охвата во времени: полные и неполные дин. ряды;
Дин. ряд будет полным, если уровни ряда определены для всех равноотстоящих дат или интервалов времени; неполный — при отсутствии некот. пок-лей и несоблюдении принципа равных интервалов.
3.По форме представл-я уровней ряда: ряды абсол. и относит.(иногда средних) величин;