- •8 Вопрос:
- •12 Вопрос: Изопроцессы
- •13 Вопрос:
- •Вывод основного уравнения мкт
- •Уравнение среднеквадратичной скорости молекулы
- •15 Вопрос: Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения
- •16 Вопрос: Число степеней свободы молекулы и закон равномерного распределения энергии по степеням свободы молекул
- •17 Вопрос: Внутренняя энергия
- •Идеальные газы
- •19 Вопрос:
- •Раздел 2. Электричество. Постоянный ток. Магнетизм.
- •24 Вопрос: Работа по перемещению заряда в электрическом поле. Потенциал
- •26 Вопрос:
- •28 Вопрос: 1.8. Электрический ток. Закон Ома
- •30 Вопрос: Закон Ома для неоднородного участка цепи
- •32 Вопрос: Закон Био - Савара - Лапласа и его применение к расчету магнитного поля
- •34 Вопрос:
- •35 Вопрос: Сила Лоренца
- •36 Вопрос: Закон полного тока
- •Ток смещения
- •37 Вопрос: Основные формулы
- •38 Вопрос: Явление электромагнитной индукции.
- •Закон Фарадея
- •40 Вопрос: Уравнения Максвелла для электромагнитного поля
- •Раздел 3. Оптика и атомная физика
- •45 Вопрос: Дифракция Света
- •47 Вопрос: фракция Фраунгофера на одной щели
- •48 Вопрос: Дифракция Фраунгофера на дифракционной решетке. Условия минимумов и максимумов.
- •Энергетическая светимость тела
- •52 Вопрос: 1.2. Законы Кирхгофа
- •53 Вопрос: Формулы Рэлея - Джинса и Планка
- •54 Вопрос: Модели атома Томсона и Резерфорда
- •55 Вопрос: Формула Бальмера
- •История создания формулы Бальмера и ее значение
- •57 Вопрос: Квантовые числа и их физический смысл
- •58 Вопрос: Состав атомного ядра
- •1919 Г. Э. Резерфорд. Ядерная реакция. 14n(α,p)17o
- •1919 Г. Э. Резерфорд. Ядерная реакция. 14n(α,p)17o
- •1932 Г. Дж. Чедвик. Открытие нейтрона
- •Нейтроны
- •Размер ядра
- •Размер ядра и закон сил
- •Характеристики свободных нейтрона и протона
- •59 Вопрос: Закон радиоактивного распада
57 Вопрос: Квантовые числа и их физический смысл
Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел. "Задайте значения квантовых чисел, и я полностью опишу свойства атома" - так может современный физик перефразировать известное изречение Архимеда.
Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.
1.
Главное квантовое число
![]() .
Это квантовое число принимает значения
.
Это квантовое число принимает значения
![]()
и определяет полную энергию электрона в любом квантовом состоянии
|
(5.37) |
Можно
отметить, что эти значения энергии
являются собственными значениями
гамильтониана (5.17a).
Поэтому в связанном состоянии электрон
в атоме водорода имеет дискретный
энергетический спектр, лежащий в области
отрицательных значений и имеющий точку
сгущения
![]() .
.
2.
Орбитальное (азимутальное) квантовое
число
![]() .
В квантовых состояниях с заданным
значением главного квантового числа
азимутальное
квантовое число может иметь следующие
значения:
.
В квантовых состояниях с заданным
значением главного квантового числа
азимутальное
квантовое число может иметь следующие
значения:
![]() .
.
Из
выводов предыдущего параграфа следует,
что стационарные волновые функции
![]() ,
описывающие различные квантовые
состояния атома, являются собственными
функциями не только оператора полной
энергии
,
описывающие различные квантовые
состояния атома, являются собственными
функциями не только оператора полной
энергии
![]() ,
но и оператора квадрата момента импульса
,
но и оператора квадрата момента импульса
![]() ,
причем
,
причем
![]() .
.
Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:
|
(5.38) |
Проанализируем эту формулу квантования
момента импульса. Сравнивая ее с условием
(5.3)
квантования момента импульса движущегося
электрона в теории Бора, можно заметить,
что эти условия не совпадают. И дело не
только в отличии числовых значений,
рассчитанных по этим формулам.
Принципиальное отличие этих соотношений
состоит в том, что в квантовой механике
возможны состояния атома с нулевым
моментом импульса. Во всех
![]() -состояниях
и, частности, в основном
-состояниях
и, частности, в основном
![]() -состоянии,
когда
-состоянии,
когда
![]() ,
по формуле (5.38)
получаем
,
по формуле (5.38)
получаем
![]() .
.
При классическом описании движения электрона в атоме по определенной траектории (орбите) в любом состоянии атом должен обладать ненулевым моментом импульса.
Опыт подтверждает существование квантовых состояний атома с нулевыми орбитальными моментами. Следовательно, опыт подтверждает, что только отказ от классического траекторного способа описания движения электрона в атоме позволяет правильно рассчитать и предсказать свойства атома. Вероятностный способ описания движения частиц в квантовой механике является единственно правильным способом описания свойств атомных систем - таков вывод современной физики.
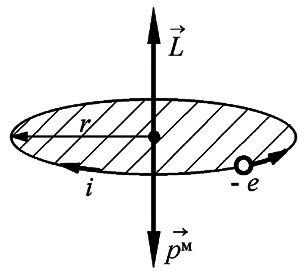
Так
как движущийся вокруг ядра электрон
является заряженной частицей, то такое
движение обуславливает протекание
некоторого замкнутого тока в атоме,
который можно охарактеризовать
орбитальным магнитным моментом![]() .
.
В
теории Бора, когда с позиции классической
теории рассматривается круговое движение
электрона по орбите радиуса
![]() со
скоростью
со
скоростью
![]() ,
величина орбитального механического
момента равна
,
величина орбитального механического
момента равна
![]() .
Если время полного оборота электрона
.
Если время полного оборота электрона
![]() ,
то такому движению соответствует
замкнутый ток
,
то такому движению соответствует
замкнутый ток
![]() ,
,
который можно охарактеризовать величиной магнитного момента
![]() .
.
Связь механического и магнитного моментов при этом определяется гиромагнитным отношением
|
(5.39) |
Так
как заряд электрона отрицателен, то для
орбитального движения направление
вектора магнитного момента
противоположно
направлению вектора механического
момента импульса
![]() (рис.
5.8).
(рис.
5.8).
Для
расчета орбитального магнитного момента
в квантовой теории следует определить
пространственную плотность электрического
тока
![]() через
плотность потока вероятностей
через
плотность потока вероятностей
![]() по
формуле:
по
формуле:
![]() .
Плотность потока вероятности при этом
можно найти по формуле (3.23),
зная волновую функцию электрона в
заданном квантовом состоянии атома.
Точный квантовомеханический расчет
гиромагнитного отношения также приводит
к формуле (5.39).
.
Плотность потока вероятности при этом
можно найти по формуле (3.23),
зная волновую функцию электрона в
заданном квантовом состоянии атома.
Точный квантовомеханический расчет
гиромагнитного отношения также приводит
к формуле (5.39).
|
Рис. 5.8. |
Итак,
в любом квантовом состоянии атом водорода
обладает не только механическим моментом
![]() ,
величина которого определяется формулой
(5.38),
но и магнитным моментом.
,
величина которого определяется формулой
(5.38),
но и магнитным моментом.
|
(5.40) |
Здесь универсальная постоянная
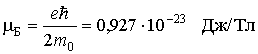
служит единицей измерения магнитных моментов атомов и называется магнетоном Бора.
Если
атом переходит из одного квантового
состояния в другое с испусканием
(поглощением) фотона излучения, то
возможны лишь такие переходы, для которых
орбитальное квантовое число
изменяется
на единицу. Это правило, согласно которому
для оптических переходов
![]() ,
называется правилом отбора. Наличие
такого правила отбора обусловлено тем,
что электромагнитное излучение (фотон)
уносит или вносит не только квант
энергии, но и вполне определенный момент
импульса, изменяющий орбитальное
квантовое число для электрона всегда
на единицу.
,
называется правилом отбора. Наличие
такого правила отбора обусловлено тем,
что электромагнитное излучение (фотон)
уносит или вносит не только квант
энергии, но и вполне определенный момент
импульса, изменяющий орбитальное
квантовое число для электрона всегда
на единицу.
3.
Магнитное квантовое число
.
В квантовом состоянии с заданным
значением орбитального квантового
числа
,
магнитное квантовое число может принимать
![]() различных
значений из ряда
различных
значений из ряда
![]() .
.
Физический смысл магнитного квантового
числа вытекает из того, что волновая
функция
![]() ,
описывающая квантовое состояние
электрона в атоме водорода, является
собственной функцией оператора проекции
момента импульса
,
описывающая квантовое состояние
электрона в атоме водорода, является
собственной функцией оператора проекции
момента импульса
![]() ,
причем
,
причем
![]() .
.
Поэтому, из общих положений квантовой
механики (см. раздел
3.5) следует, что проекция момента
импульса электрона на выделенное в
пространстве направление
![]() может
иметь только определенные значения,
равные
может
иметь только определенные значения,
равные
|
(5.41) |
Направление в пространстве обычно выделяется внешним полем (например, магнитным или электрическим), в котором находится атом.
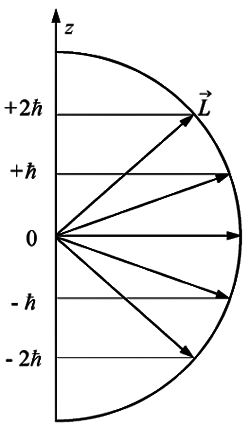
Так как формула (5.41) квантования проекции механического момента соответствует вполне определенным направлениям ориентации в пространстве вектора (рис. 5.9), то эту формулу называют обычно формулой пространственного квантования.
С точки зрения классического представления об электронной орбите, с учетом перпендикулярности вектора к плоскости орбиты, соотношение (5.41) определяет возможные дискретные расположения электронных орбит в пространстве по отношению к направлению внешнего поля.
|
Рис. 5.9. |
Отмеченная выше связь механического и магнитного моментов атома позволяет с учетом (5.41) записать также возможные значения проекции магнитного момента атома на выделенное направление :
|
(5.42) |
зависящие от значения магнитного квантового числа .

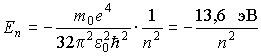 .
.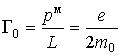 .
.