
- •8 Вопрос:
- •12 Вопрос: Изопроцессы
- •13 Вопрос:
- •Вывод основного уравнения мкт
- •Уравнение среднеквадратичной скорости молекулы
- •15 Вопрос: Закон Максвелла о распределении молекул идеального газа по скоростям и энергиям теплового движения
- •16 Вопрос: Число степеней свободы молекулы и закон равномерного распределения энергии по степеням свободы молекул
- •17 Вопрос: Внутренняя энергия
- •Идеальные газы
- •19 Вопрос:
- •Раздел 2. Электричество. Постоянный ток. Магнетизм.
- •24 Вопрос: Работа по перемещению заряда в электрическом поле. Потенциал
- •26 Вопрос:
- •28 Вопрос: 1.8. Электрический ток. Закон Ома
- •30 Вопрос: Закон Ома для неоднородного участка цепи
- •32 Вопрос: Закон Био - Савара - Лапласа и его применение к расчету магнитного поля
- •34 Вопрос:
- •35 Вопрос: Сила Лоренца
- •36 Вопрос: Закон полного тока
- •Ток смещения
- •37 Вопрос: Основные формулы
- •38 Вопрос: Явление электромагнитной индукции.
- •Закон Фарадея
- •40 Вопрос: Уравнения Максвелла для электромагнитного поля
- •Раздел 3. Оптика и атомная физика
- •45 Вопрос: Дифракция Света
- •47 Вопрос: фракция Фраунгофера на одной щели
- •48 Вопрос: Дифракция Фраунгофера на дифракционной решетке. Условия минимумов и максимумов.
- •Энергетическая светимость тела
- •52 Вопрос: 1.2. Законы Кирхгофа
- •53 Вопрос: Формулы Рэлея - Джинса и Планка
- •54 Вопрос: Модели атома Томсона и Резерфорда
- •55 Вопрос: Формула Бальмера
- •История создания формулы Бальмера и ее значение
- •57 Вопрос: Квантовые числа и их физический смысл
- •58 Вопрос: Состав атомного ядра
- •1919 Г. Э. Резерфорд. Ядерная реакция. 14n(α,p)17o
- •1919 Г. Э. Резерфорд. Ядерная реакция. 14n(α,p)17o
- •1932 Г. Дж. Чедвик. Открытие нейтрона
- •Нейтроны
- •Размер ядра
- •Размер ядра и закон сил
- •Характеристики свободных нейтрона и протона
- •59 Вопрос: Закон радиоактивного распада
36 Вопрос: Закон полного тока
Датский физик X.Эрстед в начале 19 века определил главный в теории электромагнетизма экспериментальный факт, он заключается в следующим, протекание по проводникам электрического тока приводит к появлению в окружающем пространстве магнитного поля.
Этот факт предоставил возможность французскому выдающемуся ученому Лмперу выразить формулировкой закон, который на сегодняшний день имеет название закона полного тока.
Проанализируем рисунок ниже, воображаемый контур L в пространстве, ограничивающий поверхность S.
На этом контуре установим направление обхода так, чтобы движение с конца вектора вдоль контура элементарной площадки dS прослеживалось в направлении против часовой стрелки.
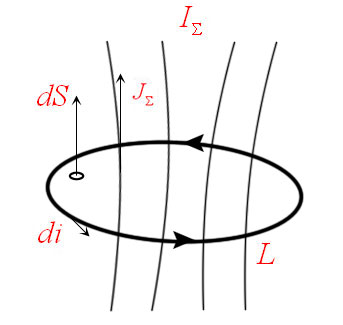
Далее
представим то, что поверхность S
пронизывается отдельной системой токов,
которая может нести как дискретный
характер (к примеру, систему отдельных
проводников), так и быть непрерывно
распределенной (электронный поток может
послужить этому примером). Не обуславливая
тем временем физической природы данных
токов, будем подразумевать для
конкретности, что они распределены
непрерывно в пространстве с кое-какой
плотностью
![]()
То теперь полный ток, пронизывающий контур, найдется в виде
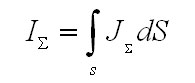
Закон
полного тока говорит о том, что циркуляция
по контуру L вектора напряженности
магнитного поля, инициированного
протеканием тока ![]() равна полному току, то есть.
равна полному току, то есть.
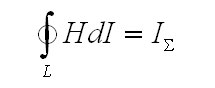
Закон полного тока формулирует соотношение выше в интегральной форме.
В том, чтобы связать плотность полного тока в данной гонке с напряженностью магнитного поля, то есть найти дифференциальную форму данного закона, надлежит употребить знаменитой теоремой Стикса из векторного анализа, которая говорит нам о том, что для каждого векторного поля А верно равенство
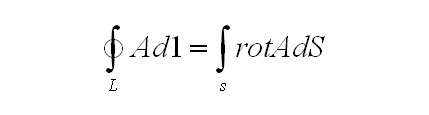
Использовав крайнюю формулу и перестроив с её помощью
![]()
будем располагать
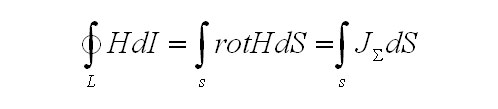
откуда получим из-за произвольности выбранного контура
![]()
Формула выше несёт в себе закон полного тока в дифференциальной форме. Заметим, что при помощи закона полного тока в интегральной форме удается разрешить ряд задач, связанных по нахождению магнитного поля заданных токов.
Ток смещения
Известен из практики факт прохождения электрического переменного тока по цепи, включающий в себя конденсатор. Значительно важным тут приходится то, что ток протекает между обкладками по пространству, в котором нет каких-либо носителей электрического заряда. Вследствие чего можно предположить, что в данной области течёт некий ток, натура которого принципиально непохожа на натуры тока проводимости, ранее освоенного. Данный ток впервые был влит в электродинамику Максвеллом, а назвал он его током смещения.
Мы видим цепь с конденсатором, представленную изображением ниже, в нём выделена замкнутая поверхность S, охватывающая одну из обкладок конденсатора.
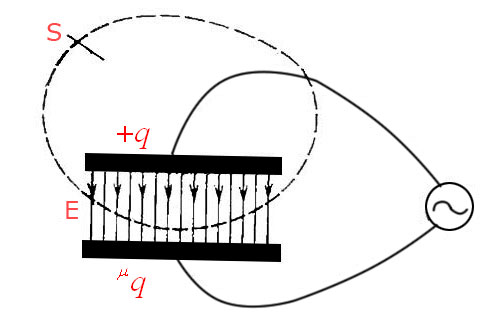
Из закона Гаусса надлежит, что если, когда между обкладками имеется вакуум,
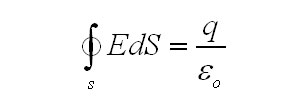
Ток в цепи в свою очередь, найдется следующим образом:
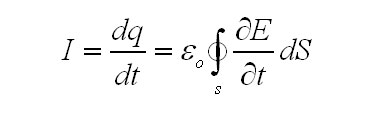
Последнее выражение показывает, что величина
![]()
обладает размерностью плотности тока, который и должен называться током смещения.
Таким образом, плотность тока смещения в вакууме
![]()
Предложением Максвелла было введение плотности тока смещения в правую часть закона полного тока наряду плотностью тока проводимости. Данное решение оказалось довольно значительным для электродинамики, поскольку при этом становилось возможным устанавить внутреннюю взаимосвязь магнитного и электрического поля. В действительности, к протеканию тока смещения, который, в свою очередь, вызывает появление магнитного поля, приводит изменение во времени электрического поля в какой-либо точке пространства.
