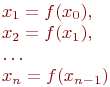- •1. Внутренняя сортировка данных методом подсчета. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •2. Внутренняя сортировка данных методом выбора. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •3. Внутренняя сортировка данных методом простых вставок. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •4. Внутренняя сортировка данных методом Шелла. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •5. Внутренняя сортировка данных методом «пузырька». Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •6. Внутренняя сортировка данных «быстрым» методом. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •7. Численное решение уравнения методом половинного деления (дихотомии). Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •Метод хорд
- •9. Численное решение уравнения методом Ньютона (касательных). Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •Метод Ньютона
- •10. Численное решение уравнения модифицированным методом Ньютона. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Модифицированный метод Ньютона
- •Модифицированный метод Ньютона (метод секущих)
- •Метод ньютона-рафсона
- •11. Численное решение уравнения методом секущих. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •Условие сходимости
- •12. Численное решение уравнения методом простых итераций. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Метод простых итераций
- •13. Численное интегрирование методом прямоугольников. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Метод прямоугольников
- •Пример реализации
- •14. Численное интегрирование методом трапеций. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Метод трапеций
- •15. Численное интегрирование методом парабол. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •Формула
- •Представление в виде метода Рунге-Кутта
- •Составная формула (формула Котеса)
- •16. Численное интегрирование методом Гаусса-Лежандра. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •17. Численное интегрирование методом Монте-Карло. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Интегрирование методом Монте-Карло
- •Обычный алгоритм Монте-Карло интегрирования
- •Геометрический алгоритм Монте-Карло интегрирования
- •Использование выборки по значимости
- •Оптимизация Применение в физике
- •18. Построение кривой по точкам. Интерполяционный полином Лагранжа. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •Определение
- •Применения
- •Случай равномерного распределения узлов интерполяции
- •Погрешность интерполирования
- •Выбор узлов интерполяции
- •20. Построение кривой по точкам. Интерполяция кубическими сплайнами. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.
- •Интерполяция кубическими сплайнами
- •Введение
- •Постановка математической задачи
- •Изложение метода
- •Метод прогонки
- •Пример: интерполирование неизвестной функции
- •Ошибка интерполяции
- •Пример: интерполяция синуса
- •Дискретное преобразование Фурье
- •Пример использования
- •Погрешность вычислений
- •Программная реализация
12. Численное решение уравнения методом простых итераций. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Метод простых итераций
В ряде случаев весьма удобным приемом уточнения корня уравнения является метод последовательных приближений (метод итераций).
Пусть с точностью необходимо найти корень уравнения f(x)=0, принадлежащий интервалу изоляции [a,b]. Функция f(x) и ее первая производная непрерывны на этом отрезке.
Для применения этого метода исходное уравнение f(x)=0 должно быть приведено к виду
|
(4.2) |
В качестве начального приближения 0 выбираем любую точку интервала [a,b].
Далее итерационный процесс поиска корня строится по схеме:
|
(4.3) |
В результате итерационный процесс поиска реализуется рекуррентной формулой (4.3). Процесс поиска прекращается, как только выполняется условие
|
(4.4) |
или число итераций превысит заданное число N.
Для того, чтобы последовательность х1, х2,…, хn приближалась к искомому корню, необходимо, чтобы выполнялось условие сходимости:
|
(4.5) |
 Рис.
4.6.
Геометрический смысл метода
Рис.
4.6.
Геометрический смысл метода
Переходим
к построению схемы алгоритма (рис.
4.7).
Вычисление функции ![]() оформим
в виде подпрограммы.
оформим
в виде подпрограммы.
 Рис.
4.7.
Схема алгоритма уточнения корня методом
итераций
Рис.
4.7.
Схема алгоритма уточнения корня методом
итераций
13. Численное интегрирование методом прямоугольников. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм. Метод прямоугольников
Словесный алгоритм метода прямоугольников:
Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.
Определяем значение yi подынтегральной функции f(x) в каждой части деления, т.е.
![]()
В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяционным многочленом степени n = 0, т.е. прямой, параллельной оси OX. В результате вся подынтегральная функция на участке [a,b] аппроксимируется ломаной линией.
Для каждой части деления определяем площадь Si частичного прямоугольника.
Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных прямоугольников.
Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага, то метод называется методом левых прямоугольников (рис.12.3). Тогда квадратурная формула имеет вид


Рис. 12.3. Метод левых прямоугольников
Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага, то метод называется методом правых прямоугольников (рис.12.4). Тогда квадратурная формула имеет вид
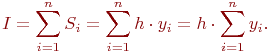

Рис. 12.4. Метод правых прямоугольников
Точность каждого метода прямоугольников имеет порядок h.
Алгоритм вычисления интеграла построим в виде итерационного процесса поиска с автоматическим выбором шага. На каждом шаге будем уменьшать шаг в два раза, то есть увеличивать число шагов n в два раза. Выход из процесса поиска организуем по точности вычисления интеграла. Начальное число шагов n=2.Схема алгоритма методов прямоугольников представлена на рис.12.5.

Рис. 12.5. Схема алгоритма метода прямоугольников (с автоматическим выбором шага)
Условные обозначения:
a,b - концы интервала,
- заданная точность,
с=0 - метод левых прямоугольников,
с=1 - метод правых прямоугольников,
S1 - значение интеграла на предыдущем шаге,
S - значение интеграла на текущем шаге.