Использование выборки по значимости

При том же количестве случайных точек, точность вычислений можно увеличить, приблизив область, ограничивающую искомую функцию, к самой функции. Для этого необходимо использовать случайные величины с распределением, форма которого максимально близка к форме интегрируемой функции. На этом основан один из методов улучшения сходимости в вычислениях методом Монте-Карло: выборка по значимости.

Оптимизация Применение в физике

Компьютерное моделирование играет в современной физике важную роль и метод Монте-Карло является одним из самых распространённых во многих областях от квантовой физики до физики твёрдого тела, физики плазмы и астрофизики.

18. Построение кривой по точкам. Интерполяционный полином Лагранжа. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для   пар чисел  , где все   различны, существует единственный многочлен   степени не более  , для которого  .

В простейшем случае ( ) — это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Определение

Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и(7,9), а также полиномы y_i l_i(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных x_j

Лагранж предложил способ вычисления таких многочленов:

где базисные полиномы определяются по формуле:

 обладают следующими свойствами:

• являются многочленами степени 

• 

•  при 

Отсюда следует, что  , как линейная комбинация  , может иметь степень не больше  , и  , Q.E.D.

Применения

Полиномы Лагранжа используются для интерполяции, а также для численного интегрирования.

Пусть для функции   известны значения   в некоторых точках. Тогда мы можем интерполировать эту функцию как

В частности,

Значения интегралов от   не зависят от  , и их можно вычислить заранее, зная последовательность  .

Случай равномерного распределения узлов интерполяции

В случае равномерного распределения узлов интерполяции   выражаются через расстояние между узлами интерполяции h и начальную точку  :

,

и, следовательно,

Подставив эти выражения в формулу базисного полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

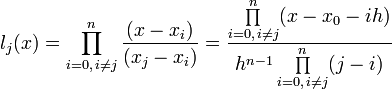
Теперь можно ввести замену переменной

и получить полином от  , который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.

19. Построение кривой по точкам. Интерполяционный полином Ньютона. Эффективность данного алгоритма. Привести фрагмент программы, поясняющий данный алгоритм.

Многочлен Ньютона интерполяционный – как и другие интерполяционные формулы (см. интерполяция), служит для построения многочлена n-й степени, который совпадает в (n+1) точке co значениями неизвестной искомой функции у =f(x).

Пусть  в  точках  х₀, х₁, …, х_n+1  значения  функции  у = f(x)  равны  соответственноу₀ = f(x₀), y₁ = f(x₁), …, y_n+1 = f(x_n+1).

Построим  интерполяционный многочлен Ньютона с помощью метода неопределенных коэффициентов. Для этого запишем искомый многочлен в виде P_n(x) = b₀ + b₁(x – x₀) + b₂(x – x₀)(x – x₁) + b₃(x – x₀)(x – x₁)(x – x₂) + … + b_n(x – x₀)…(x – x_n). (1)

Последовательно подставляя в формулу (1) вместо х данные значения х₀, х₁, ...,х_n+1, получим для нахождения неопределенных коэффициентов b₀, b₁, ..., b_n«треугольную» систему уравнений 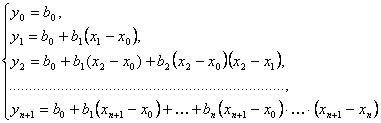(при подстановке в равенство (1) вместо х числа х₀ в правой части равенства обратились в нуль все слагаемые, кроме первого: там везде был множитель (х – х₀), обратившийся  в нуль; при подстановке х = х₁ обратились в нуль все слагаемые, кроме первого и второго – они содержат множитель (х – х₁) и т.д.).

Полученную систему удобно решать: из первого её уравнения находим свободный член искомого многочлена b₀; подставив его во второе уравнение, находим коэффициент  b₁ при первой степени х в искомом многочлене: и т.д.  

Для интерполяционного многочлена Ньютона можно выписать явные выражения коэффициентов через данные задачи, а также и оценки точности замены неизвестной функции f(x) этим многочленом.

Интерполяция полиномами Лагранжа и Ньютона

Постановка задачи

Пусть задана функция  .  Пусть заданы точки   из некоторой области  . Пусть значения функции   известны только в этих точках. Точки   называют узлами интерполяции.  - шаг интерполяционной сетки. Задача интерполяции состоит в поиске такой функции   из заданного класса функций, что 

Метод решения задачи

Полином Лагранжа

Представим интерполяционную функцию в виде полинома где   - полиномы степели n вида: Очевидно, что   принимает значение 1 в точке   и 0 в остальных узлах интерполяции. Следовательно в точке   исходный полином принимает значение  Таким образом, построенный полином   является интерполяционным полиномом для функции   на сетке  . 

Полином Ньютона

Интерполяционный полином в форме Лагранжа не удобен для вычислений тем, что при увеличении числа узлов интерполяции приходится перестраивать весь полином заново. Перепишем полином Лагранжа в другом виде: где   - полиномы Лагранжа степени i ≤ n. Пусть    . Этот полином имеет степень i и обращается в нуль при  .  Поэтому он представим в виде: , где   - коэффициент при  . Так как   не входит в  , то   совпадает с коэффициентом при   в полиноме  . Таким образом из определения   получаем: где  Препишем формулу   в виде  Рекуррентно выражая   пролучам окончательную формулу для полинома:  Такое представление полинома удобно для вычисления, потому что увеличение числа узлов на единицу требует добавления только одного слагаемого.