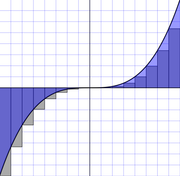
Цикл с предусловием

Цикл с предусловием — цикл, который выполняется пока истинно некоторое условие, указанное перед его началом. Это условие проверяется до выполнения тела цикла, поэтому тело может быть не выполнено ни разу (если условие с самого начала ложно). В большинстве процедурных языков программирования реализуется оператором while, отсюда его второе название — while-цикл.

На языке Си:

while(<условие>)

{

<тело цикла>

}

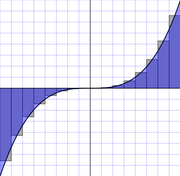
Цикл с постусловием

Цикл с постусловием — цикл, в котором условие проверяется после выполнения тела цикла. Отсюда следует, что тело всегда выполняется хотя бы один раз. в Си — do…while.

На языке Си:

do

{

<тело цикла>

}

while(<условие продолжения цикла>)

В трактовке условия цикла с постусловием в разных языках есть различия. В Паскале и языках, произошедших от него, условие такого цикла трактуется как условие выхода (цикл завершается, когда условие истинно, в русской терминологии такие циклы называют ещё «цикл до»), а в Си и его потомках — как условие продолжения (цикл завершается, когда условие ложно, такие циклы иногда называют «цикл пока»).

12

Функции пользователя в языке C++

Функция — самостоятельная единица программы, спроектированная для реализации конкретной задачи. Каждая функция должна иметь имя, которое используется для вызова. Имя функции main(), которая обязательно присутствует в любой С-программе, зарезервировано. В программе на С могут присутствовать несколько функций, причем функция main() необязательно должна быть первой. Но с функции main() всегда начинается выполнение любой С-программы.

При вызове функции ей могут быть переданы данные посредством аргументов. Функция может возвращать значение, которое и есть основной результат выполнения функции; этот результат подставляется на место вызова функции, где бы этот вызов не встретился в программе. Могут быть определены функции, которые не имеют никаких параметров и не возвращают никакого значения. Тем не менее действие таких функций может состоять в изменении внешних переменных или статических переменных или выполнением каких-либо других действий, не связанных с данными.

13

Работа с файлами в C++.

Описание функций работы с файломи находятся в библиотеке stdio.h

Сначала надо создать указатель на переменную типа FILE ( FILE* file; ).

Открытие файла производится вызовом функции fopen ( file = fopen( file_name, "w" ); )

Первый параметр этой функции - имя файла, второй - указывает в каком режиме должен быть открыт файл. "w" - открыть для записи, "r" - открыть для чтения, "a" - дополнение файла( это наиболее используемые режимы, хотя есть и другие ). Запись и считывание данных из файла осуществляется следующими функциями : fputc, fputs, fgetc, fgets, fprintf, fscanf( описание этих функций смотрите в stdio.h).

Закрытие файла осуществляется вызовом функции fclose ( fclose( file ); ).

14

Работа с файлами в C++. Форматный ввод/вывод.

Работа с файлами в C ( работает и в C++ )..

#include

#include

void main( void )

{

FILE *file;

char* file_name = "file.txt";

char load_string[50] = "none";

file = fopen( file_name, "w" );

fputs( "string", file );

fclose( file );

file = fopen( file_name, "r" );

if( file != 0 )

{

fgets( load_string, 50 , file );

cout

Описание функций работы с файломи находятся в библиотеке stdio.h

Сначала надо создать указатель на переменную типа FILE ( FILE* file; ).

Открытие файла производится вызовом функции fopen ( file = fopen( file_name, "w" ); )

Первый параметр этой функции - имя файла, второй - указывает в каком режиме должен быть открыт файл. "w" - открыть для записи, "r" - открыть для чтения, "a" - дополнение файла( это наиболее используемые режимы, хотя есть и другие ). Запись и считывание данных из файла осуществляется следующими функциями : fputc, fputs, fgetc, fgets, fprintf, fscanf( описание этих функций смотрите в stdio.h).

Закрытие файла осуществляется вызовом функции fclose ( fclose( file ); ).

Форматный ввод - функция scanf.

Осуществляющая ввод функция scanf является аналогом printf и позволяетпроводить в обратном направлении многие из тех же самыхпреобразований. Функция

scanf(control, arg1, arg2, ...)

читает символы из стандартного ввода, интерпретирует их в соответствиис форматом, указанном в аргументе control, и помещает результаты востальные аргументы. Управляющий аргумент описывается ниже; другиеаргументы, каждый из которых должен быть указателем, определяют,куда следует поместить соответствующим образом преобразованный ввод.

Управляющая строка обычно содержит спецификации преобразования,которые используются для непосредственной интерпретации входныхпоследовательностей. Управляющая строка может содержать:

пробелы, табуляции или символы новой строки ("символы пустыхпромежутков"), которые игнорируются.

Обычные символы (не %), которые предполагаются совпадающими соследующими отличными от символов пустых промежутков символамивходного потока.

Спецификации преобразования, состоящие из символа %, необязательногосимвола подавления присваивания *, необязательного числа, задающегомаксимальную ширину поляи символа преобразования.

Спецификация преобразования управляет преобразованием следующего поляввода. Нормально результат помещается в переменную, которая указываетсясоответствующим аргументом. Если, однако, с помощью символа * указаноподавление присваивания, то это поле ввода просто пропускается иникакого присваивания не производится. Поле ввода определяется какстрока символов, которые отличны от символов простых промежутков;оно продолжается либо до следующего символа пустого промежутка, либопока не будет исчерпана ширина поля, если она указана. Отсюдаследует, что при поиске нужного ей ввода, функция scanf будетпересекать границы строк, поскольку символ новой строки входит вчисло пустых промежутков.

Символ преобразования определяет интерпретацию поля ввода; согласнотребованиям основанной на вызове по значению семантики языка "Си"соответствующий аргумент должен быть указателем. Допускаются следующиесимволы преобразования:

d

на вводе ожидается десятичное целое; соответствующий аргумент долженбыть указателем на целое.

o

на вводе ожидается восьмеричное целое (с лидирующим нулем или без него);соответствующий аргумент должен быть указателем на целое.

x

на вводе ожидается шестнадцатеричное целое (с лидирующими 0х или безних); соответствующий аргумент должен быть указателем на целое.

h

на вводе ожидается целое типа short; соответсвующий аргумент долженбыть указателем на целое типа short.

c

ожидается отдельный символ; соответствующий аргумент должен бытьуказателем на символы; следующий вводимый символ помещается вуказанное место. Обычный пропуск символов пустых промежутков в этомслучае подавляется; для чтения следующего символа, который неявляется символом пустого промежутка, пользуйтесь спецификациейпреобразования %1s.

s

ожидается символьная строка; соответствующий аргумент должен бытьуказателем символов, который указывает на массив символов, которыйдостаточно велик для принятия строки и добавляемого в конце символа \0.

f

ожидается число с плавающей точкой; соответствующий аргумент долженбыть указателем на переменную типа float.

e

символ преобразования е является синонимом для f. Формат вводапеременной типа float включает необязательный знак, строку цифр,возможно содержащую десятичную точку и необязательное поле экспоненты,состоящее из буквы е, за которой следует целое, возможно имеющее знак.

Перед символами преобразования d, о и х может стоять l, которая означает, что в списке аргументов должен находиться указатель на переменнуютипа long, а не типа int. Аналогично, буква l можетстоять перед символами преобразования е или f, говоря о том, что всписке аргументов должен находиться указатель на переменную типаdouble, а не типа float.

Например, обращение

int 1; float x; char name[50]; scanf("&d %f %s", &i, &x, name);

со строкой на вводе

25 54.32e-1 thompson

приводит к присваиванию i значения 25, x - значения 5.432 и name -строки "thompson", надлежащим образом законченной символом \ 0.Эти три поля ввода можно разделить столькими пробелами, табуляциямии символами новых строк, сколько вы пожелаете. Обращение

int i; float x; char name[50]; scanf("%2d %f %*d %2s", &i, &x, name);

с вводом

56789 0123 45a72

присвоит i значение 56, x - 789.0, пропустит 0123 и поместит вname строку "45". При следующем обращении к любой процедуре вводарассмотрение начнется с буквы а. В этих двух примерах nameявляется указателем и, следовательно, перед ним не нужно помещатьзнак &.

В качестве другого примера перепишем теперь элементарный калькуляториз главы 4,используя для преобразования ввода функцию scanf:

#include <stdio.h> main() /* rudimentary desk calculator */ { double sum, v; sum =0; while (scanf("%lf", &v) !=EOF) printf("\\t%.2f\n", sum += v); }

Выполнение функции scanf заканчивается либо тогда, когда онаисчерпывает свою управляющую строку, либо когда некоторый элементввода не совпадает с управляющей спецификацией. В качестве своегозначения она возвращает число правильно совпадающих и присвоенныхэлементов ввода. Это число может быть использовано для определенияколичества найденных элементов ввода. При выходе на конец файлавозвращается EOF; подчеркнем, что это значение отлично от 0, чтоследующий вводимый символ не удовлетворяет первой спецификации вуправляющей строке. При следующем обращении к scanf поисквозобновляется непосредственно за последним введенным символом.

Заключительное предостережение: аргументы функции scanf должны бытьуказателями. Несомненно наиболее распространенная ошибкасостоит в написании

scanf("%d", n);

вместо

scanf("%d", &n);

Форматный вывод - функция printf

Две функции: printf для вывода и scanf для ввода (следующий раздел)позволяют преобразовывать численные величины в символьноепредставление и обратно. Они также позволяют генерировать иинтерпретировать форматные строки. Мы уже всюду в предыдущихглавах неформально использовали функцию printf; здесь приводитсяболее полное и точное описание. Функция

printf(control, arg1, arg2, ...)

преобразует, определяет формат и печатает свои аргументы встандартный вывод под управлением строки control. Управляющая строкасодержит два типа об'ектов: обычные символы, которые просто копируютсяв выходной поток, и спецификации преобразований, каждая из которыхвызывает преобразование и печать очередного аргумента printf.

Каждая спецификация преобразования начинается с символа % изаканчивается символом преобразования. Между % и символомпреобразования могут находиться:

знак минус, который указывает о выравнивании преобразованногоаргумента по левому краю его поля.

Строка цифр, задающая минимальную ширину поля. Преобразованноечисло будет напечатано в поле по крайней мере этой ширины, а еслинеобходимо, то и в более широком. Если преобразованный аргумент имеетменьше символов, чем указанная ширина поля, то он будет дополнен слева(или справа, если было указано выравнивание по левому краю)заполняющимисимволами до этой ширины. Заполняющим символом обычно является пробел,а если ширина поля указывается с лидирующим нулем, то этим символомбудет нуль (лидирующий нуль в данном случае не означает восьмеричнойширины поля).

Точка, которая отделяет ширину поля от следующей строки цифр.

Строка цифр (точность), которая указывает максимальное числосимволов строки, которые должны быть напечатаны, или число печатаемыхсправа от десятичной точки цифр для переменных типа float илиdouble.

Модификатор длины l, который указывает, что соответствующийэлемент данных имеет тип long, а не int.

Ниже приводятся символы преобразования и их смысл:

d

аргумент преобразуется к десятичному виду.

o

аргумент преобразуется в беззнаковую восьмеричную форму(без лидирующего нуля).

x

аргумент преобразуется в беззнаковую шестнадцатеричную форму(без лидирующих 0х).

u

аргумент преобразуется в беззнаковую десятичную форму.

c

аргумент рассматривается как отдельный символ.

s

аргумент является строкой: символы строки печатаются до тех пор,пока не будет достигнут нулевой символ или не будет напечатаноколичество символов, указанное в спецификации точности.

e

аргумент, рассматриваемый как переменная типа float или double,преобразуется в десятичную форму в виде [-]m.nnnnnne[+-]хх, гдедлина строки из n определяется указанной точностью. Точность поумолчанию равна 6.

f

аргумент, рассматриваемый как переменная типа float или double,преобразуется в десятичную форму в виде [-]mmm.nnnnn, где длинастроки из n определяется указанной точностью. Точность поумолчанию равна 6.Отметим, что эта точность не определяетколичество печатаемых в формате f значащих цифр.

g

используется или формат %е или %f, какой короче;незначащие нули не печатаются.Если идущий за % символ не является символом преобразования,то печатается сам этот символ; следовательно,символ % можнонапечатать, указав %%.

Большинство из форматных преобразований очевидно и былопроиллюстрировано в предыдущих главах. Единственным исключением являетсято, как точность взаимодействует со строками. Следующая таблицадемонстрирует влияние задания различных спецификаций на печать"hello, world" (12 символов). Мы поместили двоеточия вокругкаждого поля для того, чтобы вы могли видеть его протяженность.

:%10s: :hello, world: :%10-s: :hello, world: :%20s: : hello, world: :%-20s: :hello, world : :%20.10s: : hello, wor: :%-20.10s: :hello, wor : :%.10s: :hello, wor:

Предостережение: printf использует свой первый аргумент для определениячисла последующих аргументов и их типов. Если количество аргументовокажется недостаточным или они будут иметь несоответственные типы, товозникнет путаница и вы получите бессмысленные результаты.

Упражнение 7-1.

Напишите программу, которая будет печатать разумным образом произвольныйввод. Как минимум она должна печатать неграфические символы ввосьмеричном или шестнадцатеричном виде (в соответствии с принятымиу вас обычаями) и складывать длинные строки.

15

Табулирование функций.

Табулирование функции — это вычисление значений функции при изменении аргумента от некоторого начального значения до некоторого конечного значения с определённым шагом. Именно так составляются таблицы значений функций, отсюда и название — табулирование. Необходимость в табулировании возникает при решении достаточно широкого круга задач. Например, при численном решении нелинейных уравнений f(x) = 0, путём табулирования можно отделить (локализовать) корни уравнения, т.е. найти такие отрезки, на концах которых, функция имеет разные знаки. С помощью табулирования можно (хотя и очень грубо) найти минимум или максимум функции. Иногда случается так, что функция не имеет аналитического представления, а её значения получаются в результате вычислений, что часто бывает при компьютерном моделировании различных процессов. Если такая функция будет использоваться в последующих расчётах (например, она должна быть проинтегрирована или продифференцирована и т.п.), то часто поступают следующим образом: вычисляют значения функции в нужном интервале изменения аргумента, т.е. составляют таблицу (табулируют), а затем по этой таблице строят каким-либо образом другую функцию, заданную аналитическим выражением (формулой). Необходимость в табулировании возникает также при построении графиков функции на экране компьютера.

16-17

Решение нелинейного уравнения. Методы хорд, метод половинного деления.

 Решение нелинейных уравнений

Метод половинного деления ~ Метод хорд

 

Нелинейные уравнения можно разделить на 2 класса - алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.

Методы решения нелинейных уравнений делятся на две группы:

1. точные методы;

2. итерационные методы.

Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Как известно, многие уравнения и системы уравнений не имеют аналитических решений. В первую очередь это относится к большинству трансцендентных уравнений. Доказано также, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраическое уравнение степени выше четвертой. Кроме того, в некоторых случаях уравнение содержит коэффициенты, известные лишь приблизительно, и, следовательно, сама задача о точном определении корней уравнения теряет смысл. Для их решения используются итерационные методы с заданной степенью точности.

Пусть дано уравнение

(1)

где:

1. Функция f(x) непрерывна на отрезке [a, b] вместе со своими производными 1-го и 2-го порядка.

2. Значения f(x) на концах отрезка имеют разные знаки (f(a)   f(b) < 0).

3. Первая и вторая производные f' (x) и f'' (x) сохраняют определенный знак на всем отрезке.

Условия 1) и 2) гарантируют, что на интервале [a, b] находится хотя бы один корень, а из 3) следует, что f(x) на данном интервале монотонна и поэтому корень будет единственным.

Решить уравнение (1) итерационным методом значит установить, имеет ли оно корни, сколько корней и найти значения корней с нужной точностью.

Всякое значение  , обращающее функцию f(x) в нуль, т.е. такое, что:

называется корнем уравнения (1) или нулем функции f(x).

Задача нахождения корня уравнения f(x) = 0 итерационным методом состоит из двух этапов:

1. отделение корней - отыскание приближенного значения корня или содержащего его отрезка;

2. уточнение приближенных корней - доведение их до заданной степени точности.

Процесс отделения корней начинается с установления знаков функции f(x) в граничных x = a и x = b точках области ее существования.

Пример 1. Отделить корни уравнения:

f(x)  x3 - 6х + 2 = 0.

(2)

Составим приблизительную схему:

х				0	1	3	
f(x)			+	+			+

Следовательно, уравнение (2) имеет три действительных корня, лежащих в интервалах [-3, -1], [0, 1] и [1, 3].

Приближенные значения корней (начальные приближения) могут быть также известны из физического смысла задачи, из решения аналогичной задачи при других исходных данных, или могут быть найдены графическим способом.

В инженерной практике распространен графический способ определения приближенных корней.

Принимая во внимание, что действительные корни уравнения (1) - это точки пересечения графика функции f(x) с осью абсцисс, достаточно построить график функции f(x) и отметить точки пересечения f(x) с осью Ох, или отметить на оси Ох отрезки, содержащие по одному корню. Построение графиков часто удается сильно упростить, заменив уравнение (1) равносильным ему уравнением:

,

(3)

где функции f₁(x) и f₂(x) - более простые, чем функция f(x). Тогда, построив графики функций у = f₁(x) и у = f₂(x), искомые корни получим как абсциссы точек пересечения этих графиков.

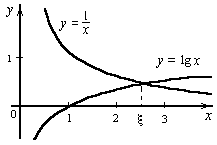
Рисунок 2.

 

Пример 2. Графически отделить корни уравнения (Рисунок 2):

x lg x = 1.

(4)

Уравнение (4) удобно переписать в виде равенства:

lg x= .

Отсюда ясно, что корни уравнения (4) могут быть найдены как абсциссы точек пересечения логарифмической кривой y = lg x и гиперболы y =  . Построив эти кривые, приближенно найдем единственный корень   уравнения (4) или определим его содержащий отрезок [2, 3].

Итерационный процесс состоит в последовательном уточнении начального приближения х₀. Каждый такой шаг называется итерацией. В результате итераций находится последовательность приближенных значений корня х₁, х₂, ..., х_n. Если эти значения с увеличением числа итераций n приближаются к истинному значению корня, то говорят, что итерационный процесс сходится.

 

Метод половинного деления

 

Для нахождения корня уравнения (1), принадлежащего отрезку [a, b], делим этот отрезок пополам. Если f  = 0 , то  =  является корнем уравнения. Если f  не равно 0 (что, практически, наиболее вероятно), то выбираем ту из половин   или , на концах которой функция f(x) имеет противоположные знаки. Новый суженный отрезок  а₁, b_1 снова делим пополам и производим те же самые действия.

Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, метод прост и надежен, всегда сходится.

Пример 3. Методом половинного деления уточнить корень уравнения

f(x) = x⁴ + 2 x³ - x - 1 = 0

лежащий на отрезке  0, 1 .

Последовательно имеем:

f(0) = - 1; f(1) = 1; f(0,5) = 0,06 + 0,25 - 0,5 - 1 = - 1,19;

f(0,75) = 0,32 + 0,84 - 0,75 - 1 = - 0,59;

f(0,875) = 0,59 + 1,34 - 0,88 - 1 = + 0,05;

f(0,8125) = 0,436 + 1,072 - 0,812 - 1 = - 0,304;

f(0,8438) = 0,507 + 1,202 - 0,844 - 1 = - 0,135;

f(0,8594) = 0,546 + 1,270 - 0,859 - 1 = - 0,043 и т. д.

Можно принять

 =  (0,859 + 0,875) = 0,867

 

Метод хорд

 

В данном методе процесс итераций состоит в том, что в качестве приближений к корню уравнения (1) принимаются значениях₁, х₂, ..., х_n точек пересечения хорды АВ с осью абсцисс (Рисунок 3). Сначала запишем уравнение хорды AB:

.

Для точки пересечения хорды AB с осью абсцисс (х = х₁, y = 0) получим уравнение:

Пусть для определенности f'' (x) > 0 при а    х    b (случай f'' (x) < 0 сводится к нашему, если записать уравнение в виде - f(x) = 0). Тогда кривая у = f(x) будет выпукла вниз и, следовательно, расположена ниже своей хорды АВ. Возможны два случая: 1) f(а) > 0 (Рисунок 3, а) и 2) f(b) < 0 (Рисунок 3, б).

   

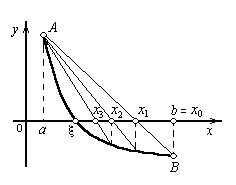
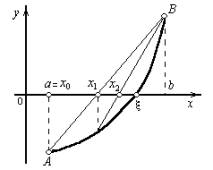
Рисунок 3, а, б.

 

В первом случае конец а неподвижен и последовательные приближения: x₀ = b;

(5)

образуют ограниченную монотонно убывающую последовательность, причем

Во втором случае неподвижен конец b, а последовательные приближения: x₀ = а;

(6)

образуют ограниченную монотонно возрастающую последовательность, причем

Обобщая эти результаты, заключаем:

1. неподвижен тот конец, для которого знак функции f (х) совпадает со знаком ее второй производной f'' (х);

2. последовательные приближения x_n лежат по ту сторону корня  , где функция f (х) имеет знак, противоположный знаку ее второй производной f'' (х).

Итерационный процесс продолжается до тех пор, пока не будет обнаружено, что

 x_i - x_{i -} 1|<  ,

где  - заданная предельная абсолютная погрешность.

Пример 4. Найти положительный корень уравнения

f(x)  x³ - 0,2 x² - 0,2 х - 1,2 = 0

с точностью  = 0,01.

Прежде всего, отделяем корень. Так как

f (1) = -0,6 < 0 и f (2) = 5,6 > 0,

то искомый корень  лежит в интервале [1, 2]. Полученный интервал велик, поэтому разделим его пополам. Так как

f (1,5) = 1,425 > 0, то 1<  < 1,5.

Так как f'' (x) = 6 x - 0,4 > 0 при 1 < х < 1,5 и f (1,5) > 0, то воспользуемся формулой (5) для решения поставленной задачи:

= 1,15;

x₁ - x₀| = 0,15 >  ,

следовательно, продолжаем вычисления;

f (х₁) = -0,173;

= 1,190;

|x₂ - x₁ = 0,04 >  ,

f (х₂) = -0,036;

= 1,198;

x₃ - x₂ = 0,008 <  .

Таким образом, можно принять  = 1,198 с точностью  = 0,01.

Заметим, что точный корень уравнения  = 1,2.

18-19

Интегрирование функций. Метод прямоугольников, трапеций.

Метод прямоугольников — метод численного интегрирования функции одной переменной, заключающийся в замене подынтегральной функции на многочлен нулевой степени, то есть константу, на каждом элементарном отрезке. Если рассмотреть график подынтегральной функции, то метод будет заключаться в приближённом вычислении площади под графиком суммированием площадей конечного числа прямоугольников, ширина которых будет определяться расстоянием между соответствующими соседними узлами интегрирования, а высота — значением подынтегральной функции в этих узлах. Алгебраический порядок точности равен 0.

Если отрезок   является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по

1. Формуле левых прямоугольников: 

2. Формуле правых прямоугольников: 

3. Формуле прямоугольников (средних): 

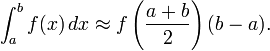
Составные квадратурные формулы

В случае разбиения отрезка интегрирования на   элементарных отрезков приведённые выше формулы применяются на каждом из этих элементарных отрезков между двумя соседними узлами. В результате, получаются составные квадратурные формулы

1. Для левых прямоугольников: 

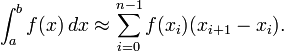
2. Для правых прямоугольников: 

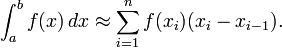
3. Для средних прямоугольников: 

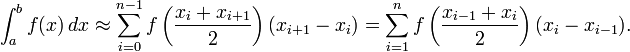
Формулу с вычислением значения в средней между двумя узлами точке можно применять лишь тогда, когда подынтегральная функция задана аналитически, либо каким-нибудь иным способом, допускающим вычисление значения в произвольной точке. В задачах, где функция задана таблицей значений остаётся лишь вычислять среднее значение между интегралами, посчитанными по формулам левых и правых прямоугольников соответственно, что приводит к составной квадратурной формуле трапеций.

Поскольку составные квадратурные формулы являются ни чем иным, как суммами, входящими в определение интеграла Римана, при   они сходятся к точному значению интеграла. Соответственно, с увеличением   точность получаемого по приближённым формулам результата возрастает.

Сравнение применения различных формул прямоугольников
Формула левых прямоугольников   Формула средних прямоугольников   Формула правых прямоугольников

Метод трапеций — метод численного интегрирования функции одной переменной, заключающийся в замене на каждом элементарном отрезке подынтегральной функции на многочлен первой степени, то есть линейную функцию. Площадь под графиком функции аппроксимируется прямоугольными трапециями. Алгебраический порядок точности равен 1.

Если отрезок   является элементарным и не подвергается дальнейшему разбиению, значение интеграла можно найти по формуле

Это простое применение формулы для площади трапеции — полусумма оснований, которыми в данном случае являются значения функции в крайних точках отрезка, на высоту (длину отрезка интегрирования). Погрешность аппроксимации можно оценить через максимум второй производной

20

Суммирование бесконечных сходящихся рядов.