77.Статистика Бозе-Эйнштейна (подсчет числа микросостояний, функция распределения).
Подсчет числа состояний в распределении Бозе-Эйнштейна. В модели Бозе-Эйнштейна в каждом квантовом состоянии может находиться произвольное число неразличимых между собой частиц. Как и при выводе распределения Ферми-Дирака, используем понятия энергетических уровней и возможных состояний в пределах отдельного уровня.
При этом условии
общее число различных распределений
частиц по
местам выражается формулой
.
Тогда общее число микросостояний на
всех энергетических уровнях:
-
число микросостояний для модели
Бозе-Эйнштейна.
Рассуждая так же, как и при выводе распределения Ферми-Дирака получим формулу:
- распределения
Бозе-Эйнштейна.
Эта формула переходит в распределение Максвелла-Больцмана в случае, когда среднее число частиц, приходящихся на одно квантовое состояние, достаточно мало.
Конкуренция между частицами при занятии состояний в статистике Ферми-Дирака чрезвычайно интенсивна, поскольку занятое какой-либо частицей состояние запрещено для других частиц. Можно в определенном смысле говорить, что частица, занимающая некоторое состояние, отталкивает от этого состояния другие частицы, как бы удерживает из на некотором удалении от этого состояния. Конкуренция между частицами ослабевает, когда число допустимых для них состояний много больше числа частиц.
В статистике Бозе-Эйнштейна такая конкуренция отсутствует: частица может занять некоторое состояние независимо от того. Занято ли оно другими частицами или свободно. Ясно, что если конкуренция в статистике Ферми-Дирака ослабевает, то ее результаты должны приближаться к результатам статистике Бозе-Эйнштейна. Это наблюдается при малом среднем числе частиц, приходящихся на одно квантовое состояние. В этом случае распределения Ферми-Дирака и Бозе-Эйнштейна совпадают и сводятся к распределению Максвелла-Больцмана.
78.Длина свободного пробега.
Молекулы газов
сталкиваются друг с другом. Между двумя
последовательными соударениями молекула
проходит путь
,
который называют длиной свободного
пробега. Естественно, что смысл имеет
только средняя длина свободного
пробега
,
которую в дальнейшем будем называть
просто длиной свободного пробега.
Припишем молекуле некоторый эффективный
диаметр
,
т.е. наименьшее расстояние, на которое
сближаются молекулы при соударении. Он
зависит от скорости, температуры, но мы
пренебрежем этим.
Ч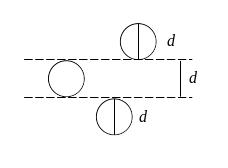
исло
соударений в цилиндре длиной
и поперечным сечением
должно быть равно
.
Т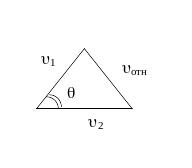
еперь
уточним эту формулу. Мы считали другие
молекулы неподвижными, но они тоже
движутся. Надо перейти к относительной
скорости, точнее взять среднюю
арифметическую скорость движения
молекул и перейти в их систему покоя (в
систему центра масс).
,
,
;
,
,
.
Переход к
относительной скорости, внесет в
полученную формулу множитель
:
- средняя длина
свободного пробега.
79.Частота столкновений в единицу времени, понятие физического вакуума.
- средняя длина свободного пробега.
Среднее число
столкновений в единицу времени
получим, если учтем, что молекула за
единицу времени будет двигаться в
ломаном цилиндре длиной
,
разделив эту длину на среднюю длину
свободного пробега, узнаем среднее
число столкновений в единицу времени:
.
Для
нормальных условий в воздухе
,
;
,
.
Понятие физического
вакуума формулируется на языке длины
свободного пробега. Вакуумом
называется состояние газа, при котором
длина свободного пробега молекул
примерно равна размерам
сосуда.
Низкий вакуум -
Средний вакуум
-
Высокий вакуум
-
(
мм. рт. ст.)
Сверхвысокий
вакуум -
(ультраразреженный газ
мм. рт. ст)