25 Локальная теорема Лапласа. Свойства функции Гаусса ср(х).

Теорема

Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико, а число p отлично от 0 и 1, тогда:

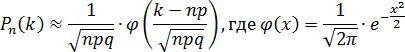
Функция φ(x) называется функцией Гаусса. Ее значения давно вычислены и занесены в таблицу, которой можно пользоваться даже на контрольных работах и экзаменах.

Функция Гаусса обладает двумя свойствами, которые следует учитывать при работе с таблицей значений:

1. φ(−x) = φ(x) — функция Гаусса — четная;

2. При больших значениях x имеем: φ(x) ≈ 0.

Локальная теорема Муавра — Лапласа дает отличное приближение формулы Бернулли, если число испытаний n достаточно велико. Разумеется, формулировка «число испытаний достаточно велико» весьма условна, и в разных источниках называются разные цифры. Например:

1. Часто встречается требование: n · p · q > 10. Пожалуй, это минимальная граница;

2. Другие предлагают работать по этой формуле только для n > 100 и n · p · q > 20.

На мой взгляд, достаточно просто взглянуть на условие задачи. Если видно, что стандартная теорема Бернулли не работает из-за большого объема вычислений (например, никто не будет считать число 58! или 45!), смело применяйте Локальную теорему Муавра — Лапласа.

К тому же, чем ближе значения вероятностей q и p к 0,5, тем точнее формула. И, наоборот, при пограничных значениях (когда p близко к 0 или 1) Локальная теорема Муавра — Лапласа дает большую погрешность, значительно отличаясь от настоящей теоремы Бернулли.

Обратите внимание: в функцию Гаусса подставляется довольно сложное число, содержащее арифметический квадратный корень и дробь. Это число обязательно надо найти еще до подстановки в функцию. Рассмотрим все на конкретных задачах:

  Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

            Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры  и , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х.

26 Интегральная теорема Лапласа. Свойство функции Лапласа ф(х). Функция Лапласа

Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

            Обозначим

            Тогда 

Т.к. интеграл  не выражается через элементарные функции, то вводится в рассмотрение функция

которая называется функцией Лапласа или интегралом вероятностей.

            Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

            Ниже показан график функции Лапласа.

             Функция Лапласа обладает следующими свойствами:

1) Ф(0) = 0;

2) Ф(-х) = - Ф(х);

3) Ф(¥) = 1.

            Функцию Лапласа также называют функцией ошибок и обозначают erf x.

 Еще используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

Ниже показан график нормированной функции Лапласа.