Операции над множествами.

• Логические.

a={1, 2, 3, 4, 5, 6, 7}

B={4, 5, 6, 7, 8, 9, 10}

BUC={2, 4, 5, 6, 7, 8, 9, 10}

C={2, 4, 6, 8, 10}

V={1, 2, 2, 4, 5, 6, 7, 8, 9, 10}

1. auc={1, 2, 3, 4, 5, 6, 7, 8, 9, 10}

2. a∩b={4, 5, 6, 7}

3. a∩(buc)={2, 4, 5, 6, 7}

4. (a∩b)uc={2, 4, 5, 6, 7, 8, 10}

5. ⌐(a∩b)={1, 2, 3, 8, 9, 10}

6. ⌐a∩⌐b={8, 9, 10}∩{1, 2, 3, }=Ø

7. AΔB A\B={1, 2, 3}

B\A={8, 9, 10}

AΔB={1, 2, 3, 8, 9, 10}

8. A\B={1, 2, 3}

AΔB=⌐(A∩B)

• Умножение.

A={1, 2, 3}

B={a, b}

1. AxB={(1, a), (1, b), (2, a), (2, b), (3, a), (3, b)}

2. BxB={(aa), (bb), (ab), (ba)}

3. Ax Ø= Ø

• Определить множество.

P(A), если A Ø { Ø }

P(A), A={ Ø, { Ø }} 4 {{ Ø } {{ Ø }} Ø { Ø { Ø }}}

• Наследником множества А называется АU{A}.

Определить наследников множеств.

1. Ø ØU{ Ø }

2. { Ø } {{ Ø }, Ø }

3. { Ø ,{ Ø }} {{ Ø }, Ø, { Ø, { Ø }}}

• Логические операции над множествами.

a={1, 2, 3, 4, 5, 6, 7}

B={4, 5, 6, 7, 8, 9, 10}

C={2, 4, 6, 8, 10}

1. A\C={1, 3, 5, 7}

2. AΔC={1, 2, 3, 8, 9, 10}

3. (A\B)U(B\A)={1, 3, 5, 7, 8, 9, 10}

4. (A∩C)\⌐B={4, 5, 6, 7, 8, 9, 10}

5. A∩(B∩⌐C)={5, 7}

6. (A\ Ø)U(A\A)={ Ø , 1, 3, 4, 5, 6, 7, 8}

7. C\A={8, 10}

• Определить истинность.

AU Ø=A 1

AΔ Ø=A 1

Если A≤B, то AUB=A 0

Если AUB=A, то B≤A 1

A\ Ø=A 1

• Используя диаграммы венна закрасить те части, которые изображают множества.

A\B

B

A

(a∩b)

B

A

(А u В) \ (А ∩ В)

B

A

au(b∩c)

C

B

A

(A∩B∩C)

C

B

A

B\(AUC)

C

B

A

(B∩C)\A

C

B

A

• Используя диаграммы венна доказать.

⌐(A∩B)=⌐AU⌐B

B

A

B

A

⌐A
⌐B

AUB

au(b∩c)= (aub)∩(auc)

(aub)∩(auc)
(aub)
(auc)

• Используя диаграммы венна нарисовать.

AΔB

B

A

⌐(AUB)

B

A

A\(A∩B)

B

A

(A∩B)ΔC

C

B

A

(AUBUC)\(A∩B∩C)

C

B

A

(A∩B)U(B∩C)U(A∩C)

C

B

A

(A\B)U(B\C)

• Доказать.

(AUB)=A∩B

B

A

(aUb)

A B

A∩(BUC)=(A∩B)U(A∩C)

A∩(BUC)

(A∩B) (A∩C)

• Задание не помню.

1. 

2. Q­­_n=

3. Q­­_n+1=

Q­­_n=

2Q_n=n(n-1)

2Q_n=

• Используя таблицу истинности доказать.

⌐(pΛq)≡⌐pv⌐q

	p	q	pΛq	⌐(pΛq)	⌐p	⌐q	⌐pv⌐q
	0	0	0	1	1	1	1
	0	1	0	1	1	0	1
	1	0	0	1	0	1	1
	1	1	1	0	0	0	0

pv(qvr)≡(pvq)vr

	p	q	r	qvr	pv(qvr)	pvq	(pvq)vr
	0	0	0	0	0	0	0
	0	0	1	1	1	0	1
	0	1	0	1	1	1	1
	0	1	1	1	1	1	1
	1	0	0	0	1	1	1
	1	0	1	1	1	1	1
	1	1	0	1	1	1	1
	1	1	1	1	1	1	1

pv(qΛr)≡(pvq)Λ(pvr)

	p	q	r	qΛr	pv(qΛr)	pvq	pvr	(pvq)Λ(pvr)
	0	0	0	0	0	0	0	0
	0	0	1	0	0	0	1	0
	0	1	0	0	0	1	0	0
	0	1	1	1	1	1	1	1
	1	0	0	0	1	1	1	1
	1	0	1	0	1	1	1	1
	1	1	0	0	1	1	1	1
	1	1	1	1	1	1	1	1

p→q≡⌐pvq

	p	q	p→q	⌐p	⌐pvq
	0	0	1	1	1
	0	1	1	1	1
	1	0	0	0	0
	1	1	1	0	1

• Не используя таблицу истинности доказать.

⌐(p→q)≡pΛ⌐q

⌐(⌐pvq)≡pΛ⌐q

⌐(pvq)≡⌐pΛ⌐q

⌐(⌐p)≡p

• Доказать, что контропозиция и инплекация эквивалентны инплекации. Без таблицы.

⌐p→⌐q≡p→q

qv⌐p ≡⌐pvq

• Доказать эквивалентность.

p≡⌐(pΛs)→(⌐sΛp)

(pΛs)v(⌐sΛp)

p≡pΛ(sv⌐s)

p≡p

• С помощью таблицы истинности доказать.

⌐(pvq)≡⌐pΛ⌐q

	p	q	pvq	⌐(pvq)	⌐p	⌐q	⌐pΛ⌐q
	0	0	0	1	1	1	1
	0	1	1	0	1	0	0
	1	0	1	0	0	1	0
	1	1	1	0	0	0	0

pΛ (qΛr)≡(pΛq) Λr

	p	q	r	qΛr	pΛ (qΛr)	pΛq	(pΛq) Λr
	0	0	0	0	0	0	0
	0	0	1	0	0	0	0
	0	1	0	0	0	0	0
	0	1	1	1	0	0	0
	1	0	0	0	0	0	0
	1	0	1	0	0	0	0
	1	1	0	0	0	1	0
	1	1	1	1	1	1	1

pΛ (qvr)≡(pΛq) v (pΛr)

	p	q	r	qvr	pΛ(qvr)	pΛq	pΛr	(pΛq)v(pΛr)
	0	0	0	0	0	0	0	0
	0	0	1	1	0	0	0	0
	0	1	0	1	0	0	0	0
	0	1	1	1	0	0	0	0
	1	0	0	0	0	0	0	0
	1	0	1	1	1	0	1	1
	1	1	0	1	1	1	0	1
	1	1	1	1	1	1	1	1

Графы.

• Найти длину и характер пути.

a b c

d e f

1. aebfcd — путь простой, длина 5

2. aecdaec — путь не простой, длина 6

3. aebcfbd — не путь

4. aecfbdafc — путь простой, длина 8

a d

b c e

1. abcabcd — путь не простой, цикл – abc, длина 6

2. bcdeca — путь не простой, длина 5

3. debace — не путь

4. decab — путь простой, длина 4

• Найти длину, характер пути и цикл.

a b c

d e f

1. dabcfbed —не путь

2. bfcedbfcb — цикл не простой, длина 8

3. abcfebfca — не путь

4. aecfbda — цикл не простой, длина 6

• Нарисовать граф.

1. K₆

a b c

d e f

2. K_1,3

a

b c d

3. K_3,4

a b c

d e f g

• Найти наименьший оющий делитель.

НОД(126, 69)

126=69*1+57

69=57*1+12

57=12*4+9

12=9*1+3

9=3*3+0

• Найти матрицы инцидентности для графов.

1. 

   	e1	e2	e3	e4	e5	e6
   V1	1	0	0	0	1	1
   V2	1	1	0	0	0	0
   V3	0	1	1	0	0	0
   V4	0	0	0	1	1	0
   V5	0	0	1	1	0	1

2. 

   	e1	e2	e3	e4	e5	e6
   V1	1	0	0	1	0	0
   V2	1	1	1	0	0	0
   V3	0	1	0	0	1	1
   V4	0	0	1	1	1	0
   V5	0	0	0	0	0	1

3. 

	e1	e2	e3	e4	e5	e6	e7	e8	e9	e10
V1	1	0	0	0	1	1	0	0	1	0
V2	1	1	0	0	0	0	1	0	0	1
V3	0	1	1	0	0	1	0	1	0	0
V4	0	0	1	1	0	0	1	0	1	0
V5	0	0	0	1	1	0	0	1	0	1

• Для этих же грфов найти матрицы смежности.

1. 	V1	V2	V3	V4	V6
   V1	0	1	0	1	1
   V2	1	0	1	0	0
   V3	0	1	0	0	1
   V4	1	0	0	0	1
   V5	1	0	1	1	0

2. 	V1	V2	V3	V4	V6
   V1	0	1	0	1	0
   V2	1	0	1	1	0
   V3	0	1	0	1	1
   V4	1	1	1	0	0
   V5	0	0	1	0	0

	V1	V2	V3	V4	V6
V1	0	1	1	1	1
V2	1	0	1	1	1
V3	1	1	0	1	1
V4	1	1	1	0	1
V5	1	1	1	1	0

• Построить граф для матрицы инцидентности.

	1	0	1	0	0	1	0	0
	0	1	0	1	0	0	1	0
	0	1	1	0	1	0	0	1
	1	0	0	1	1	0	0	0
	0	0	0	0	0	1	1	1

• По матрице смежности построить граф.

	0	0	1	0	1	0
	0	0	1	0	1	1
	1	1	0	1	0	0
	0	0	1	0	1	1
	1	1	0	1	0	0
	0	1	0	1	0	0

V₁

• Построить граф определяющий расписание группы нашей в качестве вершин и дни недели. Две вершины соединены, если в этот день есть этот предмет.

1 – физика

2 – дискретная математика

3 – физкультура

4 – основы экономической теории

5 – начертательная геометрия

6 – математический анализ

7 – программирование

8 – технология программирования

9 – иностранный язык

e

• Для указанного графа найти матрицу смежности и используя ее найти пути длинной 2 и 3.

b

a

d

c

	a	b	c	d	e
a	0	0	1	1	0
b	0	0	1	1	0
c	1	1	0	1	1
d	1	1	1	0	1
e	0	0	1	1	0

ace, ade, acb, adb, acd, adc, bca, bcd, bce, bda, bdc, bde, cad, cbd, cda, cdb, cde, ced, …

aced, acbd, acdb, adbc, adcb, adec, acde, adce, bcad, bced, bcde, bcda, bdec, bdac, bdca, bdce, …

• Доказать утверждение:

Пусть G ориентированный граф с вершинами v₁, v₂, v₃, …, v_n и матрицей смежности A. Из вершины v₁ в вершину v_j тогда существует m путей длинны 1≤k≤n, когда A^k_ij=m. A^k_ij — элемент матрицы A^k на пересечении i — строки и j — столбца.

Доказательство:

A^k_ij=m

1. k=1 A^k_ij=1

2. k=n A^k_ij=m_n

3. k=n+1 A_ijⁿ⁺¹=m_n+1

A_ijⁿ⁺¹=(Aⁿ_*A)_ij=A_i1ⁿ_*A_1j+A_i2ⁿ_*A_2j+…= _ikⁿ_*A_kj=m_n+1

• сколько натуральных чисел меньше 700 делится на 3; на 5; и на 3, и на 5.

699/5=139 на 5

699/3=233 на 3

699/3/5=46 и на 3, и на 5

• сколько существует способов избрания президента, вице – президента, секретаря и казночея студенческого клуба среди 8 человек 4курса, 10 человек 3курса, 15 человек 2курса и 20человек 1курса, если:

1. нет ограничений;

2. президентом может быть только человек 4курса;

3. никто с 4курса не может быть вице – президентом;

4. учащийся на 1курсе могут быть только секретарем.

1. 53!/49!

2. 8*52*51*50

3. 52*51*50*45

4. 33*32*31*50

• Сколько существует 4 – значных чисел, если по крайней мере 2 цифры в числе совпадают.

C³₁₀=10/(7!*3!)

• Сколько существует различных функций из 6 элементного множества в 3 элементном множестве.

6!/3!=20*6=120

• Сколько существует бинарных строк длинны 7.

1. Нет ограничений;

2. Первый и последний бит совпадает;

3. Содержащие две и более единицы.

1. 2⁷

2. 2⁶

3. 2⁵-1

• Сколькими способами можно числа меньше 10 так, чтобы 4 было сразу после 5 или 5 сразу после 4.

16*7!

• Сколько целых чисел между 1 и 401 делятся на 5 или 7.

400/5=80 на 5

400/7=57 на 7

400/7/5=11 и на 5, и на 7

80+57-11=126

Ответ: 126.

Делятся на 6 или на 10.

400/6=66 на 6

400/10=40 на 10

66+40-13=93 ответ.

• Сколько существует натуральных чисел содержащих не более 5 цифр.

1. Первая цифра 3;

2. Последняя цифра 5;

3. Или первая 3, или последняя 5;

4. Ни первая 3, ни последняя 5.

1. 11111

2. 10000

3. 20000

4. 79999

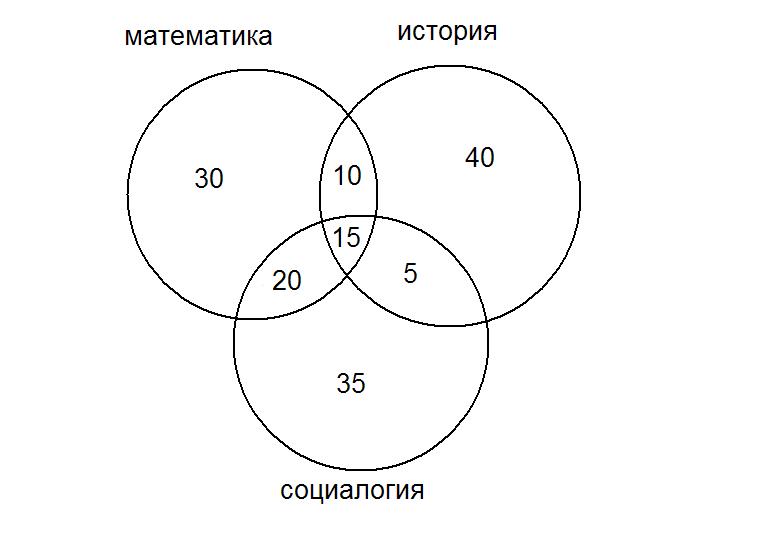
• В группе из 200 студентов 75 студентов изучают математику, 70 историю, 75 социологию, 35 математику и социологию, 25 математику и историю, 20 историю и социологию, 15 все трипредмета.

1. Сколько человек изучаетхотя бы один предмет;

2. Только одиниз трех;

3. Историю или математику ,но не социологию;

4. Не изучают 2 из 3;

5. Не изучают математику или историю.

1. 155

2. 105

3. 70

4. 165

5. 80

• Сколько целых чисел между 1 и 1001

а) делятся на 10, но не делятся на 40;

б) делятся на 10, но не делятся на 14.

г) Между 1 и 2003 делятся на 4, 5 или 6.

а) 1000/10-1000/40=75

б) 1000/10-1000/70=86

г) 500+400+333-100-166-66+33=934

• А) Сколько 3-значных чисел можно образовать используя цифры 2, 3, 4, 5, 6, 7, 8, 9;

Б) Сколько таких чисел меньше 450;

В) Сколько среди них четных чисел ;

Г) Сколько из них делятся на 4.

А) 7³=343

Б) 1*3*7+2*7*7=119

В) 7*7*4=196

Г) 7*14=98

• Сколько существует восьми битных строк содержащих 3 нуля и 5 единиц.

8!/(5!*3!)=56

• Сколько существует способов вытащить 13 картиз станлартной колоды, содержащей 52 карты, если

А) нет ограничений;

Б) 6 карт одной масти;

В) 7 карт одной масти;

Г) 8 карт одной масти;

Д) 9 карт одной масти.

А) 52!/(13!*39!)

Б) 39!*4/((39-7)!*7!)

В) 13!/(7!*6!)

Г) 13!/(8!*5!)

Д) 13!/(9!*4!)

• Сколько различных колекций из 10 монет можно собрать из монет стоимостья 1, 5, 10, 25, 50

(n+k+1)!/(n!(k-1)!)=14!/(10!4!)=1001

• Если в урне имеется 20 красных, 20 зеленых и 20 синих шаров, то сколькими различными способами можно выбрать 10 шаров.

12!/(10!2)=66

• Человек покупает 12 различных игрушек для 4 детей.

А) сколькими способами он может разделить игрушки;

Б) сколькими способами можно разделить игрушки поровну.

А) (12+3)!/(12!*3!)=455

Б) (3+11)!/(3!*11!)=364

• Решитьнайти рекуррентные функции.

А) a_n=n²a_n-1- a_n-2

Б) a_n=a²_n-1-a_n-2

В) a_n=a_n-1+ a_n-2

Г) a_n=a_n-1+3a_n-2*a­­­­­_n-3

Д) a_n=a_n-1+3a_{n-2­­­­­}­­-na_n-3

а, в, д

• Найти общее решение для рекурсивных отношений.

А) a_n-3a_n-1=0

Б) a_n+3a_n-1=0

В) a_n=-a_n-1-6a_n-2

Г) a_n=a_n-1-3a_n-2

_­А) rⁿ-3r^n-1=0

r-3=0

r=3

a_n=c3ⁿ

Б) r+3=0

r=-3

a_n=c(-3)ⁿ

В) rⁿ= -r^n-1­_­+6r^n-2

r=-3;3

a_n=c(-3)^n-1+dr^n-2

Г) rⁿ= -r^n-1­_­+3r^n-2

r² -r-3 =0

r=(1+-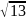 )/2

a_n=c(1- )/2+d(1+ )/2