
- •36. Балансовая модель. Общий принцип построения балансовых моделей.
- •37. Принципиальная схема межотраслевого баланса. Построение и характеристики е элементов.
- •38 И 40. Модель межотраслевого баланса в.Леонтьева. Модель натуральной и стоимостной форме.
- •39. Понятие продуктивности матрицы прямых материальных затрат.
36. Балансовая модель. Общий принцип построения балансовых моделей.
Балансовые модели
предназначены для анализа и планирования
производства и распределения продукции
на различных уровнях — от отдельного
предприятия до народного хозяйства в
целом. Если вспомнить историю народного
хозяйства как Советского Союза и России,
так и других развитых стран, то можно
наблюдать, что в экономики многих
государств, в разное время случались
экономические кризисы разных крайностей
от кризисов перепроизводства (США,
середина ХХ века), до дефицита (Россия,
конец ХХ века). Все эти экономические
кризисы связаны с нарушением баланса
между производством и потреблением. Из
этих фактов видно, что баланс между
произведенной продукцией и потреблением
является важными критериями как для
макроэкономики, так и для микроэкономики.
Экономико-математические
модели баланса пытались выстроить
многие экономисты и математики с самого
начала возникновения проблемы, однако,
наиболее полную балансовую модель
удалось построить в 1936 г. американским
экономи стом В. Леонтьевым (который
после революции эмигрировал в США и за
свою модель получил Нобелевскую премию
в области экономики). Эта модель позволяла
рассчитать баланс между несколькими
взаимодействующими отраслями, хотя ее
можно легко обобщить и для организаций
микроэкономики, например, для вычисления
баланса между несколькими взаимодействующими
предприятиями или между подразделениями
одного предприятия (например, цехами
одного завода).
Цель
балансового анализа — ответить на
вопрос, возникающий в макроэкономике
и связанный с эффективностью ведения
многоотраслевого хозяйства: каким
должен быть объем производ ства каждой
из п
отраслей, чтобы удовлетворить все
потребности в продукции этой отрасли?
При этом каждая отрасль выступает, с
одной стороны, как производитель
некоторой продукции; а с другой — как
потребитель продукции и своей, и
произведенной другими отраслями.
Предположим, что рассматривается п
отраслей
промышленно сти, каждая из которых
производит свою продукцию. Пусть общий
объем произведенной продукции i
-й отрасли равен
![]() .
Полная стоимость продукции произведенной
i-й
отраслью будем называть валовым продуктом
этой отрасли. Теперь рассмотрим, на что
тратится продукция, производимая
отраслью. Часть продукции идет на
внутрипроизводственное потребление
данной отраслью и потребление другими
отраслями, связанными с этой отраслью.
Количество продукции i-й
отрасли, предназначенной на для целей
конечного потребления (вне сферы
материального производства) личного и
общественного j-й
отраслью обозначим
.
Полная стоимость продукции произведенной
i-й
отраслью будем называть валовым продуктом
этой отрасли. Теперь рассмотрим, на что
тратится продукция, производимая
отраслью. Часть продукции идет на
внутрипроизводственное потребление
данной отраслью и потребление другими
отраслями, связанными с этой отраслью.
Количество продукции i-й
отрасли, предназначенной на для целей
конечного потребления (вне сферы
материального производства) личного и
общественного j-й
отраслью обозначим
![]() .
Оставшаяся часть предназначена для
реализацию во внешнюю сферу. Эта часть
называется конечным продуктом. Пусть
i-ая
отрасль производит
.
Оставшаяся часть предназначена для
реализацию во внешнюю сферу. Эта часть
называется конечным продуктом. Пусть
i-ая
отрасль производит
![]() конечного
продукта.
Рассмотрим
процесс производства за некоторый
период времени (например, год). Так, как
валовой объем продукции любой i-й
отрасли равен суммарному объему
продукции, потребляемой n
отраслями, и конечного продукта, то
уравнение баланса между производством
и потреблением будет иметь вид:
конечного
продукта.
Рассмотрим
процесс производства за некоторый
период времени (например, год). Так, как
валовой объем продукции любой i-й
отрасли равен суммарному объему
продукции, потребляемой n
отраслями, и конечного продукта, то
уравнение баланса между производством
и потреблением будет иметь вид:
![]() ,
(i=1,2,…,n)
(7.1)
Уравнения (1) называются соотношениями
баланса.
Можно также рассчитать такой показатель,
как чистую продукцию
,
(i=1,2,…,n)
(7.1)
Уравнения (1) называются соотношениями
баланса.
Можно также рассчитать такой показатель,
как чистую продукцию
![]() ,
которая равна разности между валовым
продуктом и суммарным потреблением
данной отраслью:
,
которая равна разности между валовым
продуктом и суммарным потреблением
данной отраслью:
![]() .
(7.2)
Все, ранее рассмотренные
показатели, можно записать в основную
балансовую таблицу:
.
(7.2)
Все, ранее рассмотренные
показатели, можно записать в основную
балансовую таблицу:
 В результате, основная балансовая
таблица, содержит четыре матрицы: матрица
межотраслевых производственных связей
В результате, основная балансовая
таблица, содержит четыре матрицы: матрица
межотраслевых производственных связей
 ,
матрицу валовой продукции
,
матрицу валовой продукции
 ,
матрицу конечной продукции
,
матрицу конечной продукции
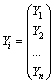 и матрицу чистой продукции
и матрицу чистой продукции
![]() .
Одной из задач балансового анализа
является определение валового продукта
,
если известно распределение конечного
.
Для этого введем коэффициенты прямых
затрат:
.
Одной из задач балансового анализа
является определение валового продукта
,
если известно распределение конечного
.
Для этого введем коэффициенты прямых
затрат:
![]() .
(7.3)
Они получаются в
результате деления всех элементов
каждого столбца матрицы
на
соответствующий элемент матрицы
межотраслевых производственных связей
Х.
Коэффициенты прямых затрат имеют смысл
количества потребления продукции j-й
отрасли, необходимой для производства
единицы продукции i-й
отраслью. Из выражения (3) можно получить:
.
(7.3)
Они получаются в
результате деления всех элементов
каждого столбца матрицы
на
соответствующий элемент матрицы
межотраслевых производственных связей
Х.
Коэффициенты прямых затрат имеют смысл
количества потребления продукции j-й
отрасли, необходимой для производства
единицы продукции i-й
отраслью. Из выражения (3) можно получить:
![]() .
Подставив последнее выражение в
соотношение баланса (1), получим:
.
Подставив последнее выражение в
соотношение баланса (1), получим:
![]() .
(7.4)
Если обозначить
матрицу коэффициентов прямых затрат
как
.
(7.4)
Если обозначить
матрицу коэффициентов прямых затрат
как
 ,
то соотношение баланса (4) в матричном
виде можно записать в виде:
,
то соотношение баланса (4) в матричном
виде можно записать в виде:
![]() .
(7.5)
Из последнего выражения можно найти
значение конечного продукта при известном
значении валового:
.
(7.5)
Из последнего выражения можно найти
значение конечного продукта при известном
значении валового:
![]() ,
(7.6)
где
,
(7.6)
где
 -
единичная матрица того же размера, что
и А.
-
единичная матрица того же размера, что
и А.
Пример 1.
Баланс четырех отраслей за предыдущий
период имеет матрицу межотраслевых
производственных связей вида
 и
матрицу валовой продукции вида
и
матрицу валовой продукции вида
 .
Необходимо определить конечный продукт
Y
и чистый продукт C
каждой отрасли.
Конечный
продукт Y
получается в результате вычитания из
каждого элемента матрицы валовой
продукции суммы элементов
соответствующих строк матрицы
.
Например, первое значение
.
Необходимо определить конечный продукт
Y
и чистый продукт C
каждой отрасли.
Конечный
продукт Y
получается в результате вычитания из
каждого элемента матрицы валовой
продукции суммы элементов
соответствующих строк матрицы
.
Например, первое значение
![]() равно
100-(10+20+15+10)=45. Чистый продукт С
получается в результате вычитания из
каждого элемента матрицы валовой
продукции Х
суммы элементов соответствующих столбцов
матрицы
.
Например, первое значение
равно
100-(10+20+15+10)=45. Чистый продукт С
получается в результате вычитания из
каждого элемента матрицы валовой
продукции Х
суммы элементов соответствующих столбцов
матрицы
.
Например, первое значение
![]() равно
100-(10+5+25+20)=40. В результате, получим основную
балансовую таблицу:
равно
100-(10+5+25+20)=40. В результате, получим основную
балансовую таблицу:
 Поставим теперь другую задачу: рассчитаем
конечный продукт каждой отрасли на
будущий период, если валовый продукт
окажется равным
Поставим теперь другую задачу: рассчитаем
конечный продукт каждой отрасли на
будущий период, если валовый продукт
окажется равным
 .
Для решения этой задачи найдем коэффициенты
прямых затрат:
.
Для решения этой задачи найдем коэффициенты
прямых затрат:
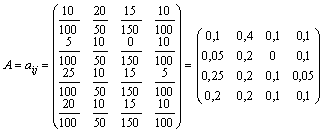 .
По формуле (6) получим
.
По формуле (6) получим
 ,
,
 Важнейшей задачей межотраслевого
баланса состоит в отыскании такого
вектора валового выпуска X,
который при известной матрице прямых
затрат А (или
при возможности рассчитать этот
показатель) обеспечивает заданный
вектор конечного продукта Y.
Из уравнения (6) можно выразить валовый
продукт:
Важнейшей задачей межотраслевого
баланса состоит в отыскании такого
вектора валового выпуска X,
который при известной матрице прямых
затрат А (или
при возможности рассчитать этот
показатель) обеспечивает заданный
вектор конечного продукта Y.
Из уравнения (6) можно выразить валовый
продукт:
![]() .
(7.7)
Матрица
.
(7.7)
Матрица
![]() называется
матрицей полных затрат. Каждый элемент
называется
матрицей полных затрат. Каждый элемент
![]() матрицы
S
есть величина валового выпуска
продукции j-й отрасли,
необходимого для обеспечения выпуска
единицы конечного продукта i-й
отрасли.
матрицы
S
есть величина валового выпуска
продукции j-й отрасли,
необходимого для обеспечения выпуска
единицы конечного продукта i-й
отрасли.
