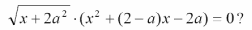Томск 2012

Над пособием работали: ученики МБОУ Лицея при ТПУ: Бокор Владимир Власов Михаил

Жульмина Маргарита Зернов Даниил Иовлев Юлий Янучковская Анастасия

Преподаватель

Алешина Ольга Борисовна

Введение

Уравнения с параметрами являются традиционно наиболее трудными задачами школьного курса алгебры и математического анализа.

Одним из методов решения уравнений с параметрами является функционально-графический. Этот метод позволяет не только исследовать свойства функций, входящих в уравнение, но и наглядно увидеть решение уравнения.

Прежде всего, при решении задач с параметрами необходимо сделать то, что делается при решении любого уравнения: привести заданное уравнение к более простому виду, если это возможно: разложить рациональное выражение на множители, избавиться от модулей, логарифмов и т.д.

Функционально-графические методы

Встречающиеся задачи на исследование уравнения или неравенства с параметром а можно записать в виде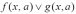 , где символ заменяет один из знаков =, > , < , , . Так как основу уравнений и неравенств составляют выражения f(x,а) и g(x,a) , то в зависимости от того, какая роль отводится параметру в задаче (параметр – фиксированное число, или параметр – переменная), запись f(x,a) рассматривается либо как семейство функций с переменной x , либо как выражение с двумя переменными x и а. В соответствии с этим используется два основных графических приема решения подобных задач: первый – построение графического образа задачи на координатной плоскости Oxy , второй – на координатных плоскостях Oxa или Oax .

§1 Координатная плоскость Oxy

задачи вида

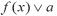
При решении задач данного вида на координатной плоскости Oxy изображают график функции f(x)= y. Тогда при заданном значении параметра a множество решений уравнения f(x)= a является проекцией на ось абсцисс точек пересечения горизонтальной прямой y=a с графиком функции f(x),а множество решений неравенства 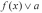является проекцией на ось абсцисс всех точек прямой y=a, ординаты которых удовлетворяют неравенству .

Возможны ситуации:

1. Прямая 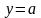не пересекает график . Следовательно, при данном значении а исходное уравнение решений не имеет.

2. Прямая пересекает график в одной или нескольких точках. Следовательно, при данном значении а можно сделать вывод о числе решений исходного уравнения, найти абсциссы точек пересечения и т.д.

Пример 1: Определите количество

различных корней уравнения

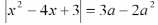
в зависимости от параметра а.

Решение:

Рассмотрим взаимное расположение графика функии 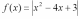и прямой 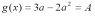на координатной плоскости Оху. Из рисунка 1 видно, что при А < 0 графики не имеют общих точек; если 0<A<1, то графики имеют четыре точки пересечения; две общие точки получаем при условии А= 0 или А>1.

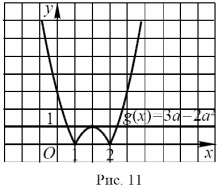
На рисунке 1 представлен случай, когда графики имеют ровно три общих точки. Данное уравнение имеет три различных корня, если выполняется условие . Отсюда а = 0,5 или а = 1. Аналогично находим а для других случаев.

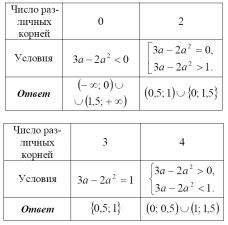
Пример 2: Найти число решений уравнения .

Решение

Заметим, что х не равно нулю. Умножим обе части уравнения на . Получим

Построим график функции .

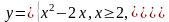
Г рафиком функции является прямая, параллельная оси ОХ.

Анализируя графическую иллюстрацию, понятно, что при а=0 одно решение, т.к. одна точка пересечения (не забываем, что х не равен нулю). При а=1 две точки пересечения графика функции и прямой, а значит и два решения. При а<0 получается одна точка пересечения, как и при а>1. Если же 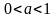, то график функции и прямая имеют три точки пересечения.

Ответ: при 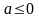, 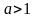одно решение,

§2 Координатные плоскости Oxa и Oax

Данный метод представляет собой некоторое обобщение графического метода решения уравнений и неравенств, основанного на использовании координатной плоскости Oxa или Oax . В последнем случае ось Ox называют координатной, ось Oa – параметрической, а плоскости Oxa и Oax – координатно-параметрическими (или КП – плоскостями).

Пример 3: При каких значениях параметра а имеет ровно два различных корня уравнения.