
Вопрос 6
Интеграл ФКП определение и свойства интеграла ФКП
Пусть
ФКП ![]() определена
в точках несамопересекающейся дуги
определена
в точках несамопересекающейся дуги ![]() ,
расположенной в
,
расположенной в ![]() –плоскости.
Дуга
–плоскости.
Дуга ![]() ориентирована
от точки
ориентирована
от точки ![]() к точке
к точке ![]() ,
причем точка
соответствует
,
причем точка
соответствует ![]() ,
точка
,
точка
![]() .
.
Рассмотрим произвольное разбиение
дуги ![]() системой
точек
системой
точек ![]() такое,
что
такое,
что ![]() ,
, ![]() и
и ![]() упорядочены
по длине дуги от точки
упорядочены
по длине дуги от точки ![]() до
конечной точки разбиения
до
конечной точки разбиения ![]() .
.
В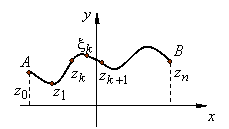 ыберем
на дуге
произвольную систему
точек
ыберем
на дуге
произвольную систему
точек ![]() так,
чтобы точка
так,
чтобы точка ![]() лежала
на дуге между точками
лежала
на дуге между точками ![]() и
и ![]() (см. рисунок).
(см. рисунок).
Сумма 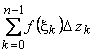 ,
где
,
где ![]() ,
называется интегральной суммой
функции
по дуге
,
соответствующей разбиению
,
называется интегральной суммой
функции
по дуге
,
соответствующей разбиению ![]() и
выбору точек системы
и
выбору точек системы ![]() ,
ее значение зависит от разбиения
и
выбора точек
.
,
ее значение зависит от разбиения
и
выбора точек
.
Обозначим ![]() –
диаметр разбиения.
–
диаметр разбиения.
Интегралом
ФКП
по дуге
называется
число (вообще говоря, комплексное
число), обозначаемое ![]() и
равное пределу интегральной суммы
функции
при
и
равное пределу интегральной суммы
функции
при ![]() ,
независимое от разбиения
и
выбора точек системы
,
т.е.
,
независимое от разбиения
и
выбора точек системы
,
т.е.
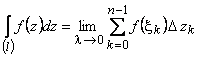 . (1)
. (1)
Доказано (см. [2]), что для непрерывной на дуге ФКП и кусочно-гладкой дуги интеграл (1) существует. Впредь будем предполагать эти условия выполненными.
Теорема
Коши для односвязной области. Если D -
односвязная ограниченная область, w = f( z) -
аналитическая в этой области функция,
то для любого кусочно-гладкого замкнутого
контура L,
лежащего в D,
интеграл от f(z) по L равен
нулю: ![]() .
Доказательство. Удивительно,
но эта важнейшая теорема непосредственно
и просто следует из условий Коши-Римана
и формулы Грина. Так как, по доказанному
выше,
.
Доказательство. Удивительно,
но эта важнейшая теорема непосредственно
и просто следует из условий Коши-Римана
и формулы Грина. Так как, по доказанному
выше,![]()
![]() ,
то, применяя к действительным криволинейным
интегралам формулу Грина, получим
,
то, применяя к действительным криволинейным
интегралам формулу Грина, получим 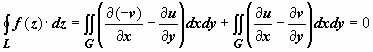 вследствие
условий Коши-Римана
вследствие
условий Коши-Римана ![]() .
Символом G в
доказательстве обозначена область,
заключённая внутри
контура L.
.
Символом G в
доказательстве обозначена область,
заключённая внутри
контура L.
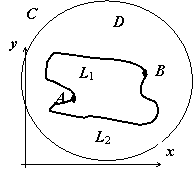 Следствие. Для
всех кусочно-гладких кривых, лежащих
внутри области D,
в которой аналитична функция w = f(z),
и имеющих общие начальную и конечную
точки, интеграл
Следствие. Для
всех кусочно-гладких кривых, лежащих
внутри области D,
в которой аналитична функция w = f(z),
и имеющих общие начальную и конечную
точки, интеграл ![]() имеет
одинаковое значение.
Доказательство
полностью повторяет доказательство Теоремы
1 раздела 16.3.3.5.1. Объединение L1∪L2− кривых
- замкнутый контур, поэтому
имеет
одинаковое значение.
Доказательство
полностью повторяет доказательство Теоремы
1 раздела 16.3.3.5.1. Объединение L1∪L2− кривых
- замкнутый контур, поэтому ![]() .
Оказывается,
что справедлива и обратная теорема
Морера: если
функция w = f(z) непрерывна
в односвязной области D и
интеграл по любому замкнутому
кусочно-гладкому контуру, лежащему
в D,
равен нулю, то функция аналитична в
области D.
.
Оказывается,
что справедлива и обратная теорема
Морера: если
функция w = f(z) непрерывна
в односвязной области D и
интеграл по любому замкнутому
кусочно-гладкому контуру, лежащему
в D,
равен нулю, то функция аналитична в
области D.
Вопрос 8 ОПЕРАЦИОННОЕ ИСЧИСЛЕНИЕ раздел математики, занимающийся главным образом алгебраическими операциями, производимыми над символами операции (или преобразования). Теория операторов. В задачу теории операторов входит подробное описание и классификация различных видов преобразований и их свойств, а также разработка символических методов, позволяющих минимизировать и упростить вычисления. Пусть D и R - действительные линейные или векторные пространства, необязательно различные. Их элементами являются векторы, поэтому сумма двух элементов и произведение элемента на скаляр определены и удовлетворяют обычным условиям, предъявляемым к векторам. Существование конечных базисов в D и R необязательно. Пусть r, вектор из R, соответствует вектору d из D. Обозначим это соответствие T(d) = r или Td = r. Тогда T называется оператором с областью определения D и областью значений R. Оператор T является дистрибутивным, если
![]() где
l и l' - любые действительные числа, а d и
d' - любые элементы из D. Если D и R -
топологические векторные пространства,
в которых ld и d + d' - непрерывные операции,
то дистрибутивный непрерывный оператор
называется линейным оператором. Если
Q содержит D и R, то T2(d) определяется как
T(T(d)) и аналогичным образом определяется
Tn(d), если все эти операции имеют смысл.
Двумя важными дистрибутивными операторами
являются операторы дифференцирования
p и интегрирования p-1. Элементами линейных
пространств D и R в этом случае будут
функции переменной x. Имеем
где
l и l' - любые действительные числа, а d и
d' - любые элементы из D. Если D и R -
топологические векторные пространства,
в которых ld и d + d' - непрерывные операции,
то дистрибутивный непрерывный оператор
называется линейным оператором. Если
Q содержит D и R, то T2(d) определяется как
T(T(d)) и аналогичным образом определяется
Tn(d), если все эти операции имеют смысл.
Двумя важными дистрибутивными операторами
являются операторы дифференцирования
p и интегрирования p-1. Элементами линейных
пространств D и R в этом случае будут
функции переменной x. Имеем
![]() где m
и n
- неотрицательные целые числа. Так как
интегрирование приводит к появлению
произвольной постоянной, p-1p необязательно
является тождественной операцией p0.
Формальные правила комбинирования
таких операторов восходят к Дж. Булю
(1815-1864); например,
где m
и n
- неотрицательные целые числа. Так как
интегрирование приводит к появлению
произвольной постоянной, p-1p необязательно
является тождественной операцией p0.
Формальные правила комбинирования
таких операторов восходят к Дж. Булю
(1815-1864); например,
![]() по
теореме Тейлора). В исчислении,
пространство D ограничено областью
определения функций f (x), тождественно
равных нулю при отрицательных x. Главную
роль играет функция 1(x), равная 0 при
отрицательных x и 1 при неотрицательных
x. Приведем некоторые "правила"
исчисления Хевисайда:
по
теореме Тейлора). В исчислении,
пространство D ограничено областью
определения функций f (x), тождественно
равных нулю при отрицательных x. Главную
роль играет функция 1(x), равная 0 при
отрицательных x и 1 при неотрицательных
x. Приведем некоторые "правила"
исчисления Хевисайда:
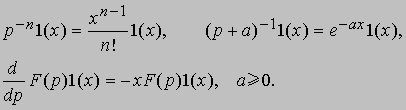 Если
n! заменить гамма-функцией Г(n + 1), то
первое из правил останется в силе и при
нецелых n.Основным результатом
операционного исчисления принято
считать теорему о композиции, или
свертке, согласно которой, если F1(p)1(x)
= f1(x) и F2(p)1(x) = f2(x), то
Если
n! заменить гамма-функцией Г(n + 1), то
первое из правил останется в силе и при
нецелых n.Основным результатом
операционного исчисления принято
считать теорему о композиции, или
свертке, согласно которой, если F1(p)1(x)
= f1(x) и F2(p)1(x) = f2(x), то
![]() Применяя
теорему о свертке к pa при a № 0, -1, -2,...,
можно определить интегрирование или
дифференцирование дробного порядка.
Например, рассмотрим выражение
Применяя
теорему о свертке к pa при a № 0, -1, -2,...,
можно определить интегрирование или
дифференцирование дробного порядка.
Например, рассмотрим выражение
![]() где
функция y(x) и ее первые n - 1 производных
обращаются в нуль при x = 0. Пусть y(x) =
Y(p)1(x), g(x) = G(p)1(x). Примем
где
функция y(x) и ее первые n - 1 производных
обращаются в нуль при x = 0. Пусть y(x) =
Y(p)1(x), g(x) = G(p)1(x). Примем
![]() Предположим,
что
f (x) = F(p)-11(x). Тогда
Предположим,
что
f (x) = F(p)-11(x). Тогда
![]() Изображением
по Лапласу функции-оригинала f (t) (или преобразованием
Лапласа функции f (t))
называется функция комплексной
переменной p,
определяемая
равенством
Изображением
по Лапласу функции-оригинала f (t) (или преобразованием
Лапласа функции f (t))
называется функция комплексной
переменной p,
определяемая
равенством
![]() .
Интеграл
в правой части этого определения
сходится абсолютно в любой точке p,
удовлетворяющей неравенству Re p ≥
σ1,
где σ1 -
произвольной число, такое, что σ1 >
σ0.
Действительно,
.
Интеграл
в правой части этого определения
сходится абсолютно в любой точке p,
удовлетворяющей неравенству Re p ≥
σ1,
где σ1 -
произвольной число, такое, что σ1 >
σ0.
Действительно, ![]() (так
к
(так
к ак | e −i Im p·t| = | cos(Im p·t)
− i sin(Im p·t)| =
1) =M | e −Re p·t|·e ·σ0t = M
e −(Re p −
σ0) t ≤ M
e −(σ1 −
σ0) t,
а интеграл
ак | e −i Im p·t| = | cos(Im p·t)
− i sin(Im p·t)| =
1) =M | e −Re p·t|·e ·σ0t = M
e −(Re p −
σ0) t ≤ M
e −(σ1 −
σ0) t,
а интеграл 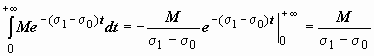 сходится.
Таким образом, мы доказали, что
изображение F(p) определено
в любой точке p,
такой что Re p >
σ0,
т.е. в полуплоскости справа от прямой
Re p =
σ0.
Как следствие, показатель скорости
роста оригинала число σ0 часто
называют абсциссой сходимости.
Заметим,
что мы доказали также, что
сходится.
Таким образом, мы доказали, что
изображение F(p) определено
в любой точке p,
такой что Re p >
σ0,
т.е. в полуплоскости справа от прямой
Re p =
σ0.
Как следствие, показатель скорости
роста оригинала число σ0 часто
называют абсциссой сходимости.
Заметим,
что мы доказали также, что ![]() :
так как | e −pt·f (t)| ≤ M
e −(Re p −
σ0) t,
то
:
так как | e −pt·f (t)| ≤ M
e −(Re p −
σ0) t,
то ![]()
![]() .
Кроме того, в оценке | e −pt·f (t)| ≤ M
e −(σ1 −
σ0) t мы
мажорировали модуль подынтегральной
функции функцией, не зависящей от p,
интеграл от которой сходится. Как и в
теории функциональных рядов, этого
достаточно, чтобы сходимость интеграла
была равномерной по переменной p,
поэтому функцию F(p) можно
дифференцировать и интегрировать по
этой переменной.
.
Кроме того, в оценке | e −pt·f (t)| ≤ M
e −(σ1 −
σ0) t мы
мажорировали модуль подынтегральной
функции функцией, не зависящей от p,
интеграл от которой сходится. Как и в
теории функциональных рядов, этого
достаточно, чтобы сходимость интеграла
была равномерной по переменной p,
поэтому функцию F(p) можно
дифференцировать и интегрировать по
этой переменной.
