- •Исчисление высказываний
- •Закон контрпозиции
- •Закон «гибельная дилемма»
- •Сведение к противоречию.
- •Представление формул для и в виде кнф
- •Критерий доказательства вывода.
- •2. Проблема непротиворечивости исчисления высказываний.
- •3. Проблема полноты исчисление высказываний.
- •4.Проблема независимости аксиом исчисления высказываний.
Сведение к противоречию.
Пусть
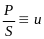 правильно построенное рассуждение с
элементарными высказываниями
правильно построенное рассуждение с
элементарными высказываниями
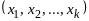 .
.
Тогда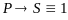 ,
отсюда
,
отсюда
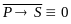 и
и
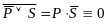 .
.
Представление формул для и в виде кнф
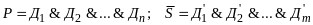 ,
где Д и Д’ – дизъюнкты.
,
где Д и Д’ – дизъюнкты.
Правило резолюций R для обработки совмещенного списка дизъюнктов.

 Объединенный
Д1
= С1
хi
Объединенный
Д1
= С1
хi
список Д2 = С2 хi

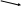 дизъюнктов
Д,
………….
С1
Сj
дизъюнктов
Д,
………….
С1
Сj

 входящих
….………
входящих
….………

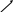 в
P
и
в
P
и
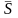 Дj
= Сj
хi
Дj
= Сj
хi
…………. Оставшийся
Дm+n список
дизъюнктов
а)
Каждый дизъюнкт из Д представим в
виде
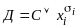 ,
где «С» все остальные переменные,
входящие в дизъюнкт, xi
выделенная переменная с отрицанием
,
где «С» все остальные переменные,
входящие в дизъюнкт, xi
выделенная переменная с отрицанием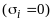 ,
либо без отрицания
,
либо без отрицания
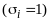 .
Из списка выделяется пара, как показано
на рисунке, с общей переменной xi
с отрицанием и без него.
.
Из списка выделяется пара, как показано
на рисунке, с общей переменной xi
с отрицанием и без него.
б) По правилу резолюции (закону резолюции), который является тавтологией (доказательство этого факта можно сделать)
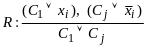 пара
дизъюнктов редуцировалась в дизъюнкт
пара
дизъюнктов редуцировалась в дизъюнкт
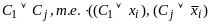 ⊦
⊦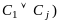 .
.
в)
Образуется новый список дизъюнктов из
дизъюнктов.
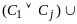 (оставшийся список дизъюнктов). Такой
список называется редуцированным.
Очевидно, что размерность редуцированного
списка по сравнению с исходным уменьшилась
на «1».
(оставшийся список дизъюнктов). Такой
список называется редуцированным.
Очевидно, что размерность редуцированного
списка по сравнению с исходным уменьшилась
на «1».
г) далее правило R применяют к редуцированному списку дизъюнктов.
д)
Останов наступает, когда в списке
остаются только два дизъюнкта вида
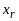 и
и
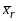 ,
либо применение R
невозможно.
,
либо применение R
невозможно.
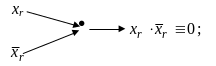
Список
дизъюнктов редуцировался в КНФ
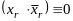
В этом случае говорят, что S логически следует из Р или S выводимо из Р.
Пример 4 Доказательство выводимости правильного умозаключения методом резолюции.

Доказательство
«от противного». Пусть следствие
(умозаключение) ложно, т.е.
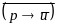 ,
тогда
,
тогда
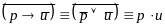 .
Список дизъюнктов –
.
Список дизъюнктов –
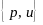 добавляется к списку дизъюнктов посылок.
добавляется к списку дизъюнктов посылок.
Алгоритм проверки выводимости правильного построенного умозаключения Вонга (Wong, 1960, США)
Выводимость P из S означает, что из множества посылок
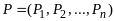 ⊦
⊦
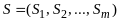 множество следствий.
множество следствий.
Это
соответствует логической формуле
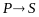 или более детально
или более детально
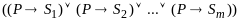 ,
где
,
где
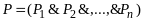 .
.
Правильно
построенному рассуждению (умозаключению)
должна соответствовать тавтология
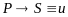 .
.
Каждая
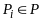 и
и
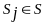 суть ППФ, построенная из связок &, ,
, .
суть ППФ, построенная из связок &, ,
, .
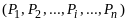 ⊦
⊦
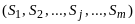 называется строкой
Вонга.
называется строкой
Вонга.
Правила обработки строки Вонга, приводящие к доказательству выводимости P ⊦ S таковы, что каждое правило суть логический закон и является тождественно истинным преобразованием.
Пусть дана строка Вонга
⊦

левая часть правая часть
строки строки
Замена импликации в строке на ДНФ:

В Рi и Sj, там, где встречается знак «».
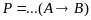 …⊦
…⊦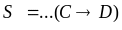 …
строка с «»
…
строка с «»
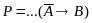 …⊦
…⊦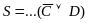 …
строка ДНФ
…
строка ДНФ
Избавление от знака отрицания « » переносом из одной части строки в другую.
а)
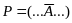 ⊦
⊦
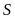 ,
добавление к правой части.
,
добавление к правой части.
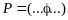 ⊦
⊦
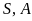 редуцированная
строка Вонга.
редуцированная
строка Вонга.
б)
Р ⊦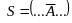 добавление к левой части
добавление к левой части
Р,А
⊦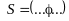 редуцированная строка Вонга.
редуцированная строка Вонга.
Перенос любой переменной в левую (правую) часть строки всегда вызывает её «отрицание».
 Избавление
от знака отрицания:
Избавление
от знака отрицания:
а)
Строка Вонга [(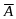 ,
B) ⊦
(C)] редуцируется в
строку
,
B) ⊦
(C)] редуцируется в
строку
[(B)
⊦ (А, C)]
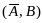 ⊦ (С) –
строка Вонга интерпретируется как
логическая формула
⊦ (С) –
строка Вонга интерпретируется как
логическая формула
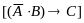 .
Редуцированная строка Вонга [
.
Редуцированная строка Вонга [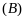 ⊦
⊦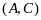 ]
и соответствующая формула
]
и соответствующая формула
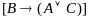 .
.
Правило редуцирования строки Вона является тождественно истинным преобразованием. Доказательство тождественности двух выражений.
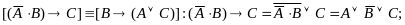
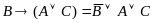
Таким
образом, если из
выводима С, то из В выводима
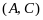
б)
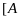 ⊦
⊦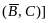 редуцируется в
редуцируется в
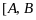 ⊦
С] и соответственно
⊦
С] и соответственно
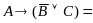
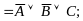
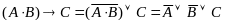
Расщепление на строки (левой и правой части строки Вонга).
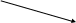 а)
а)
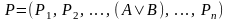 ⊦ S
; расщепление левой части
⊦ S
; расщепление левой части
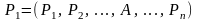 ⊦ S;
⊦ S;
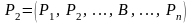 ⊦ S
⊦ S

 б)
б)
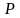 ⊦
⊦
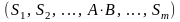 ;
расщепление правой части
;
расщепление правой части
⊦
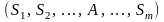 ;
⊦
;
⊦
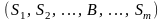
Выводимость (тавтология, тождественная истинность каждой строки должна быть доказана).
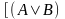 ⊦
⊦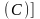 ;
расщепление –
;
расщепление –
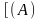 ⊦
и
⊦
и
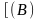 ⊦
;
⊦
;
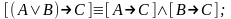
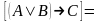
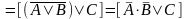 ;
;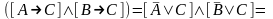
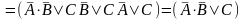
Замена логических связок на «,» (правило перечисления).
Строка Вонга
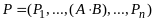 ⊦
⊦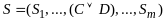
редуцируется в строку
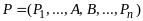 ⊦
⊦