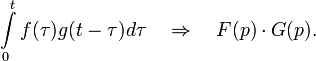Показательное (экспоненциальное распределение)
Показательным называют распределение непрерывной случайной величины Х которое
описывается следующей дифференциальной функцией
Экспоненциальное распределение для непрерывных случайных величин является
аналогом распределения Пуассона для дискретных случайных величин и имеет
следующий вид.
вероятность попадания случайной величины Х на интервал (α;β)
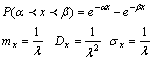
Следует отметить, что время безотказной работы удовлетворяется именно
показательному закону, а поэтому это понятие часто используется в понятии
надежности.
№15 Теорема Ляпунова.
Пусть
с 
,…
последовательность попарно независимых
случайных величин с математическими
ожиданиями M
и
дисперсиями D
,
причём эти величины обладают следующими
двумя свойствами:
1)
Cуществует такое число L, что для любого
i имеет место неравенство 
,
т, е. все значения случайных величин,
как говорят, равномерно ограничены,
относительно математических ожиданий;
2)
Сумма 
неограниченно
растёт при 
Тогда
при достаточно большом n сумма 
имеет
распределение, близкое к нормальному.
Пусть 
и 
математическое
ожидание и дисперсия случайной
величины
.
Тогда
Где 
— интеграл
вероятности.Ξερω/
№9 Решение ДУ с помощью операционного исчисления
Линейность
Изображение линейной комбинации функций равно линейной комбинации изображений с теми же коэффициентами.
где a и b – произвольные комплексные числа.
Теорема подобия
где a>0.
Дифференцирование оригинала
Дифференцирование изображения
Интегрирование оригинала
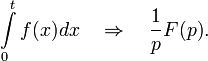
Интегрирование изображения
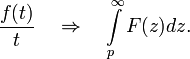
Теорема смещения
Теорема запаздывания
Теорема умножения (свёртки)
