
Т еорема Вычетов.
Основная
теорема о вычетах. Пусть функция f(z)
аналитична во всех точках ограниченной
замкнутой области ![]() ,
границей которой является контур L, за
исключением конечного числа особых
точек z1, z2, z3, …, zn, расположенных внутри
L. Тогда
,
границей которой является контур L, за
исключением конечного числа особых
точек z1, z2, z3, …, zn, расположенных внутри
L. Тогда 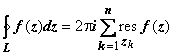 .
.
Док-во.
Окружим каждую особою точку zk, k = 1, 2, …,n
контуром ![]() таким, чтобы все контуры лежали в области
D и не пересекались. В области, ограниченной
контурами L,
таким, чтобы все контуры лежали в области
D и не пересекались. В области, ограниченной
контурами L, ![]() ,
функция аналитична, поэтому по 19.6.2.2.
Теореме Коши для многосвязной области
,
функция аналитична, поэтому по 19.6.2.2.
Теореме Коши для многосвязной области
![]() .
По определению вычета,
.
По определению вычета, ![]() ,
следовательно,
,
следовательно, 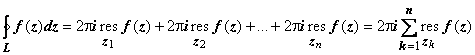 ,
что и требовалось доказать.
,
что и требовалось доказать.
№11 Основные формулы теории вероятности.
Вероятность суммы двух событий вычисляется по формуле (теорема сложения)
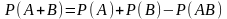 .
.
События А и В называются несовместными (непересекающимися), если они не могут произойти одновременно АВ=. Если события несовместны, то
Р(АВ) = 0 и Р(А + В) = Р(А) + Р(В).
Условная вероятность и теорема умножения.
Такую вероятность (вероятность А при условии В) обозначают Р(А|В) и вычисляют с помощью одной из двух формул:
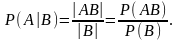
Из этой формулы вытекает формула для вероятности произведения двух событий (теорема умножения)
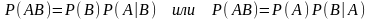 .
.
Формула умножения для трех событий:
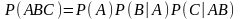 .
.
Независимость событий.
два события A и B независимы, если справедливо равенство
Р(АВ) = Р(А) Р(В).
Противоположные
события.
Если
одно из двух противоположных событий
обозначено через A, то другое принято
обозначать![]()
![]() .
.
З а м е ч а н и е 1. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают через q. Таким образом, в силу предыдущей теоремы
p + q = l
З а м е ч а н и е 2. При решении задач на отыскание вероятности события А часто выгодно сначала вычислить вероятность противоположного события, а затем найти искомую вероятность по формуле
![]() .
.
№13 Последовательность независимых испытаний. Формула Бернулли. наивероятнейшее число наступления события. Формула Пуассона
Пусть
проводится серия из n испытаний,
в каждом из которых событие А может
наступить с одной и той же вероятностью p или
не наступить с вероятностью q=1-p,
независимо от номера испытания и
результата предыдущего опыта. Такие
серии опытов называются последовательностью
независимых испытаний или схемой
Бернулли. В связи со схемой Бернулли
рассматриваются такие задачи: 1) найти
вероятность того, что в серии из n испытаний
событие А наступит ровно k раз: ![]() ;
2) найти вероятность того, что в серии
из n испытаний событие А наступит
не менее чем
;
2) найти вероятность того, что в серии
из n испытаний событие А наступит
не менее чем ![]() раз
и не более, чем
раз
и не более, чем ![]() раза:
раза: ![]()
Указанные вероятности находят по формуле Бернулли:
![]()
![]()
Если число n велико, а p не слишком мало, то для вычисления вероятности можно воспользоваться приближенными (асимптотическими) формулами Муавра-Лапласа (локальная теорема Муавра-Лапласа; интегральная теорема Муавра-Лапласа).
Локальная теорема Муавра – Лапласа:
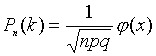 ,
где
,
где 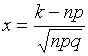 и
и 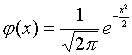
Интегральная теорема Муавра – Лапласа:
![]() ,
где
,
где 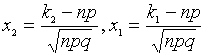
![]()
Функции j(´) и Ф(х) табулированы, то есть таблицы значений этих функций приведены в каждом учебнике по теории вероятностей. Можно указать некоторые свойства этих функций:j(-x)=j(x); Ф(-х)=-Ф(х); Ф(0)=0; Ф(х) ® 0,5 при х ® ¥.
Если число испытаний n велико, а вероятность появления события А в каждом испытании мала, то для вычисления вероятности появления k раз события А в серии из n испытаний можно воспользоваться формулой Пуассона
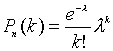 ,
где l=n×p.
,
где l=n×p.
Число ![]() успехов,
при котором достигается наибольшая из
возможных вероятностей, называется
наивероятнейшим числом успехов. Оно
определяется как целое число на
промежутке np – q£ m £ np+p.
успехов,
при котором достигается наибольшая из
возможных вероятностей, называется
наивероятнейшим числом успехов. Оно
определяется как целое число на
промежутке np – q£ m £ np+p.
Формула Бернулли
Теорема: Если
Вероятность p наступления
события Α в
каждом испытании постоянна, то
вероятность ![]() того,
что событие A наступит k раз
в n независимых
испытаниях, равна:
того,
что событие A наступит k раз
в n независимых
испытаниях, равна: ![]() ,
где
,
где ![]() .
.
Наивероятнейшее число наступления события
Число k0 называют наивероятнейшим, если вероятность того, что событие наступит в этих испытаниях k0 раз, превышает вероятности остальных возможных исходов испытаний.
Наивероятнейшее число k0 определяют из двойного неравенства
np-q≤k0≤np+p,
причем:
а) если число nр-q — дробное, то существует одно наивероят нейшее чиcло k0;
б) если число nр-q — целое, то существует два наивероятнейших числа, а именно: k0 и k0+1;
в) если число nр—целое, то наивероятнейшее число k0 = nр.
