
- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
25,26) Двойные интегралы Определение и основные свойства
Определение.
Пусть в области
определена функция
 .
Разобьем область
сетью гладких кривых на конечное число
областей
.
Разобьем область
сетью гладких кривых на конечное число
областей
 .
Возьмем произвольно в каждой области
.
Возьмем произвольно в каждой области
 по точке
по точке
 .
Обозначим через
.
Обозначим через
 площадь фигуры
,
а через
площадь фигуры
,
а через
 наибольший из диаметров частичных
областей
(диаметром точечного множества называется
точная верхняя граница расстояний между
двумя произвольными точками множества).
Сумму
наибольший из диаметров частичных
областей
(диаметром точечного множества называется
точная верхняя граница расстояний между
двумя произвольными точками множества).
Сумму
 .
.
будем называть интегральной суммой для функции в области . Конечный предел интегральных сумм при называется двойным интегралом функции в области и обозначается символом
 . (1)
. (1)
Функция, имеющая интеграл, называется интегрируемой в .
Геометрический
смысл двойного интеграла (1) – это объем
тела, ограниченного снизу – плоской
фигурой
 ,
сверху – поверхностью
,
сверху – поверхностью
 ,
а с боков – цилиндрической поверхностью
с образующими, параллельными оси
,
а с боков – цилиндрической поверхностью
с образующими, параллельными оси

Утверждение. Интегрируемая функция ограничена.
(без доказательства)
Теорема. Всякая непрерывная в ограниченной замкнутой области функция интегрируема.
(без доказательства)
Свойства интегрируемых функций и двойных интегралов. Аддитивность.
Теорема.
Если область
,
в которой задана функция
кусочно-гладкой кривой разложена на
две области
 и
и
 ,
то из интегрируемости функции во всей
области
следует ее интегрируемость на частях,
и обратно – из интегрируемости функции
в обеих областях
и
вытекает интегрируемость в
.
При этом
,
то из интегрируемости функции во всей
области
следует ее интегрируемость на частях,
и обратно – из интегрируемости функции
в обеих областях
и
вытекает интегрируемость в
.
При этом
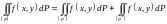 .
.
Теорема. Если ограниченная в функция имеет разрывы разве лишь на конечном числе гладких кривых, то она интегрируема в .
Линейность.
Если
функции
и
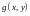 интегрируемы в
,
то для любых чисел
и
линейная комбинация
интегрируемы в
,
то для любых чисел
и
линейная комбинация
 также интегрируема, причем
также интегрируема, причем
 .
.
Интегрирование неравенств.
Если
для интегрируемых в
функций
и
выполнено неравенство
 ,
то
,
то
 .
.
Оценка модуля интеграла.
Если
функция
интегрируема в
,
то интегрируемой будет и функция
 ,
причем
,
причем
 .
.
Лемма
(об
оценке интеграла). Если интегрируемая
в
функция удовлетворяет неравенству
 ,
то
,
то
 .
.
27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
Теорема.
Если для функции
,
определенной в прямоугольнике
 ,
существует двойной интеграл
,
существует двойной интеграл
 и – при каждом постоянном значении
из
- интеграл
и – при каждом постоянном значении
из
- интеграл
 ,
,
то
существует также повторный интеграл
 и выполняется равенство
и выполняется равенство
 .
.
Схема
доказательства.
Разобьем
отрезки
и
 соответственно на части
и
соответственно на части
и
 .
Тогда прямоугольник
разобьется на части
.
Тогда прямоугольник
разобьется на части
 .
Для площадей этих частей справедлива
формула
.
Для площадей этих частей справедлива
формула
 .
.
Имеем


Меняя
роли переменных
и
 ,
можно, разумеется, доказать и формулу
,
можно, разумеется, доказать и формулу
 .
.
Приведение двойного интеграла к повторному в случае криволинейной области.
Теорема.
Если функция
непрерывна в области
,
ограниченной снизу и сверху двумя
гладкими кривыми
 и
и
 ,
а с боков – прямыми
,
а с боков – прямыми
 и
,
то выполняется равенство
и
,
то выполняется равенство
 . (2)
. (2)
Доказательство. Возьмем
 ,
,  ,
, 
и
определим в прямоугольнике
 функцию
функцию
 .
.
Функция
 ограничена на
и может иметь разрывы только в точках,
лежащих на гладких кривых
и
ограничена на
и может иметь разрывы только в точках,
лежащих на гладких кривых
и
 .
Следовательно, она интегрируема на
,
причем
.
Следовательно, она интегрируема на
,
причем
 . (3)
. (3)
Очевидно также, что при каждом существует интеграл
 . (4)
. (4)
Таким образом, для функции на выполнены все условия предыдущей теоремы и справедлива формула
 . (5)
. (5)
Подставив (3) и (4) в (5), получим (2).
Область,
описанная в условиях теоремы называется
«правильной в направлении оси
 ».
».
Если
функция
будет непрерывной в области
,
ограниченной слева и справа двумя
гладкими кривыми
 и
и
 ,
а снизу и сверху – прямыми
,
а снизу и сверху – прямыми
 и
и
 ,
то выполняется равенство
,
то выполняется равенство
 .
.
Такая
область называется «правильной в
направлении оси
 ».
».
В случае более сложного контура область можно попробовать разложить на конечное число областей рассмотренных типов.
