
- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
Уравнение
![]() (1)
(1)
называется
уравнением
в полных дифференциалах,
если его левая часть является полным
дифференциалом некоторой функции
![]() ,
т.е.
,
т.е.
![]() .
.
Теорема.
Если
функции
![]() непрерывны
в некоторой односвязной области
непрерывны
в некоторой односвязной области
![]() ,
то условие
,
то условие
![]()
является необходимым и достаточным для того, чтобы выражение
![]()
было полным дифференциалом функции .
Если
известна функция, полным дифференциалом
которой является левая часть уравнения
(1), то все решения этого уравнения имеют
вид
![]() ,
где
,
где
![]() -
произвольная постоянная.
-
произвольная постоянная.
Чтобы найти функцию нужно воспользоваться равенствами
![]() .
(2)
.
(2)
Интегрируя первое из этих равенств по x, определим функцию с точностью до произвольной дифференцируемой функции переменного y:
![]() ,
(3)
,
(3)
где
![]() -
произвольная дифференцируемая функция.
Функция
-
произвольная дифференцируемая функция.
Функция
![]() ,
такая что
,
такая что
![]() .
Дифференцируя (3) по y, с учетом второго
равенства из (2) получаем уравнение для
определения
:
.
Дифференцируя (3) по y, с учетом второго
равенства из (2) получаем уравнение для
определения
:
![]() .
.
Пример
1.
Решить уравнение
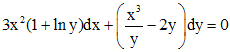 .
.
Решение.
Так как
![]()
во
всех точках полуплоскости
![]() ,
то данное уравнение является уравнением
в полных дифференциалах. Найдем функцию
такую,
что
,
то данное уравнение является уравнением
в полных дифференциалах. Найдем функцию
такую,
что
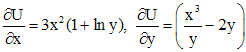 .
(4)
.
(4)
Проинтегрировав первое равенство из (4) по x, получим:
![]() .
.
Для нахождения продифференцируем по y полученное соотношение и подставим во второе равенство (4):
![]() .
.
Тогда
![]() откуда,
откуда,
![]() .
Значит
.
Значит
![]() .
.
Решение данного уравнения запишется в виде:
![]() .
.
Для интегрирования уравнений вида (1) иногда применяют метод, состоящий в выделении полных дифференциалов из разных групп слагаемых, стоящих в левой части уравнения. Для выделения полных дифференциалов используют формулы:
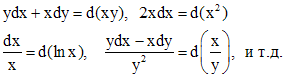
43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:
![]() где
p(x)
и h(y)
− непрерывные функции.
Рассматривая
производную y'
как отношение дифференциалов
где
p(x)
и h(y)
− непрерывные функции.
Рассматривая
производную y'
как отношение дифференциалов
![]() ,
перенесем dx
в правую часть и разделим уравнение на
h(y):
,
перенесем dx
в правую часть и разделим уравнение на
h(y):
![]()
Разумеется,
нужно убедиться, что h(y)
≠ 0. Если найдется число x0,
при котором h(x0)
= 0, то это число будет также являться
решением дифференциального уравнения.
Деление на h(y)
приводит к потере указанного решения.
Обозначив
![]() ,
запишем уравнение в форме:
,
запишем уравнение в форме:
![]()
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:
![]()
где C − постоянная интегрирования. Вычисляя интегралы, получаем выражение
![]()
описывающее общее решение уравнения с разделяющимися переменными.
Пример 1
Решить
дифференциальное уравнение
![]() .
.
Решение.
В данном случае p(x) = 1 и h(y) = y(y +2). Разделим уравнение на h(y) и перенесем dx в правую часть:
![]()
Заметим, что при делении мы могли потерять решения y = 0 и y = −2 в случае когда h(y) равно нулю. Действительно, убедимся, что y = 0 является решением данного дифференциального уравнения. Пусть
![]()
Подставляя это в уравнение, получаем: 0 = 0. Следовательно, y = 0 будет являться одним из решений. Аналогично можно проверить, что y = −2 также является решением уравнения. Вернемся обратно к дифференциальному уравнению и проинтегрируем его:
![]()
Интеграл в левой части можно вычислить методом неопределенных коэффициентов:
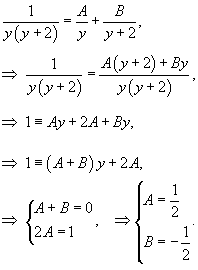
Таким образом, мы получаем следующее разложение рациональной дроби в подыинтегральном выражении:
![]()
Следовательно,
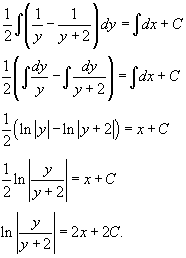
Переименуем константу: 2C = C1. В итоге, окончательное решение уравнения записывается в виде:
![]()
Общее решение здесь выражено в неявном виде. В данном примере мы можем преобразовать его и получить ответ в явной форме в виде функции y = f(x,C1), где C1 − некоторая константа. Однако это можно сделать не для всех дифференциальных уравнений.
