
- •Рациональные дроби. Простейшие рациональные дроби и их интегрирование
- •Интегрирование рациональных дробей
- •Необходимое и достаточное условие интегрируемости
- •Интегрируемость непрерывных функций
- •Свойства определенного интеграла (об изменении знака, свойства линейности и аддитивности). Найдите…
- •Определенный интеграл
- •Классы интегрируемых функций.
- •Свойства определенного интеграла
- •Интеграл с переменным верхним пределом
- •Формула интегрирования по частям.
- •Замена переменной в определенном интеграле.
- •Площадь криволинейной трапеции.
- •17. Интеграл по симметричному промежутку для четной и нечетной функции
- •18. Вычисление площадей фигур с помощью определенного интеграла. Вывод формулы.
- •19. Вычисление длины дуги плоской кривой с помощью определенного интеграла. Вывод формулы.
- •20. Вычисление объема тела по площади поперечного сечения. Объем тела вращения. Вывод формулы.
- •21) Несобственные интегралы по бесконечному промежутку.
- •25,26) Двойные интегралы Определение и основные свойства
- •Свойства интегрируемых функций и двойных интегралов. Аддитивность.
- •Линейность.
- •Оценка модуля интеграла.
- •27) Вычисление двойного интеграла Приведение двойного интеграла к повторному в случае прямоугольной области.
- •28. Полярная система координат и переход к ней под знаком двойного интеграла.
- •34) Необходимый признак сходимости числового ряда (доказать)-
- •37) Лнду (Метод Лагранжа).
- •38) Дифференциальные уравнения высшего порядка, допускающие понижение порядка.
- •39) Однородные дифференциальные уравнения первого порядка: определение, методы решения.
- •40) Линейные неоднородные дифференциальные уравнения первого порядка: определение, методы решения.
- •41) Линейные неоднородные дифференциальные уравнения высшего порядка с постоянными коэффициентами и специальной правой частью.
- •42)Дифференциальные уравнения в полных дифференциалах: определение, метод решения.
- •Теорема.
- •43) Дифференциальные уравнения с разделяющимися переменными: определение, решение.
- •44) Дифференциальные уравнения первого порядка: определение, общее решение, теорема единственности, задача Коши. Решить задачу Коши для дифференциального уравнения…
- •Теорема существования и единственности решения задачи Коши
1). Определение первообразной функции, пример. Теорема о множестве первообразных. Понятие неопределенного интеграла. Найти интеграл
Функция F(x) называется первообразной функцией для данной функции f(x), если для любого x из области определения f(x) выполняется равенство
F'(x)=f(x) или dF(x)=f(x)dx.
:
Множество F(x) + C всех первообразных
функций для данной функции f (x) , где C
принимает все возможные числовые
значения, называется неопределенным
интегралом от функции f (x)и обозначается
символом![]()
Таким
образом, по определению,
![]()
Если
существует первообразная для функции
 на промежутке
на промежутке
 ,
то множество первообразных на
называется неопределенным интегралом
от
и обозначается
,
то множество первообразных на
называется неопределенным интегралом
от
и обозначается
 ..
..
2) Свойства неопределенного интеграла. Формулировка теорем. Одну из теорем, по выбору, докажите. Непосредственное интегрирование. Примеры. Оцените интеграл.
1.Производная
неопределенного интеграла равна
подынтегральной функции, а его дифференциал
— подынтегральному выражению.
Действительно![]()
2.Неопределенный
интеграл от дифференциала функции f (x) равен
функции f (x)
с точностью
до постоянного слагаемого, т.
е.
![]()
3.Постоянный
множитель в подынтегральном выражении
можно выносить за знак неопределенного
интеграла, т.е.
![]()
4.Неопределенный
интеграл алгебраической суммы конечного
числа функций равен алгебраической
сумме неопределенных интегралов этих
функций, т.е.![]() .
.
5.интеграл от дифференциальной функции равен самой функции плюс некоторая константа.
6. Линейное преобразование аргумента подынтегральной функции при-
водит
к следующему равенству: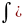 f(ax
+ b)
dx
=1\a
F(ax
+ b)
+ C,
f(ax
+ b)
dx
=1\a
F(ax
+ b)
+ C,
где F(x) – первообразная для f(x)..
Теорема 1. У всякой непрерывной на промежутке [a, b] функции имеется первообразная.
Доказательство этой теоремы будет дано далее.
Нетрудно видеть, что, если функция F(x) есть первообразная для f(x), то функция F(x) + C при любом постоянном C также является первообразной для f(x). В то же время никаких других первообразных, кроме функций вида F(x) + C, у f(x) уже быть не может. Действительно, если F1(x) есть какая-то первообразная для f(x), то производная разности F1(x) - F(x) будет всюду на [a, b] равняться нулю, а тогда сама разность есть величина постоянная, т. е.
F1(x) - F(x) = C и F1(x) = F(x) + C.
Если
F(x) есть первообразная функция для f(x),
то функция двух аргументов x и C, равная
F(x) + C, называется неопределенным
интегралом функции f(x) и обозначается
символом![]() Таким образом, неопределенный интеграл
какой-нибудь функции представляет собой
общий вид первообразных функций для
этой функции. Величина C, входящая в
определение неопределенного интеграла,
называется "произвольной постоянной".
Придавая ей то или иное закрепленное
значение, можем получить из неопределенного
интеграла любую первообразную.
Таким образом, неопределенный интеграл
какой-нибудь функции представляет собой
общий вид первообразных функций для
этой функции. Величина C, входящая в
определение неопределенного интеграла,
называется "произвольной постоянной".
Придавая ей то или иное закрепленное
значение, можем получить из неопределенного
интеграла любую первообразную.
Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.
3). 3. Метод подстановки и метод интегрирования по частям. Формулировка, доказательство.
Интегрирование с помощью подстановки
Теорема. Пусть F(z) есть на каком-нибудь промежутке [p, q] первообразная функция для функции f(z). Если φ(x) есть дифференцируемая функция, заданная на промежутке [a, b] и удовлетворяющая неравенствамp ≤ φ(x) ≤ q, то сложная функция F[φ(x)] будет первообразной для функции f[φ(x)]φ'(x).
В
самом деле, дифференцируя сложную
функцию y = F[φ(x)],
мы должны ввести промежуточный
аргумент z = φ(x).
Тогда y = F(z), z = φ(x)
и ![]()
![]()
![]() .
Так как F'(z)
= f(z),
то
.
Так как F'(z)
= f(z),
то ![]()
![]()
![]() ,
чем и доказана теорема.
,
чем и доказана теорема.
Доказанную теорему можно формулировать и так: если
![]()
![]()
то
![]()
![]()
![]()
Отсюда следует
Первое правило подстановки. Чтобы вычислить интеграл
![]()
![]()
записывая его в форме
![]()
![]()
заменяем здесь φ(x) на z, вычисляем полученный интеграл и в найденном ответе производим обратную замену z на φ(x).
Интегрирование по частям
Пусть u и v две дифференцируемые функции от х. Тогда, как известно, дифференциал произведения uv вычисляется по следующей формуле :d(uv)=udv+vdu.Отсюда, интегрируя, получаем или
.
 (1)
(1)
Последняя формула называется формула интегрирования по частям. Эта формула чаще всего применяется к интегрированию выражений которые можно так представить в виде произведения двух сомножителей u и dv, чтобы отыскать функцию v по её дифференциалу dv и вычисления интеграла составляли в совокупности задачу более простую, чем непосредственное вычисление интеграла . Умение разбивать разумным образом данное подынтегральное выражение на множители u и dv вырабатывается в процессе решения задачи , и мы покажем на ряде примеров, как это делается4.Интегрирование рациональных функций. Определения рациональной дроби, правильной и неправильной. Формулировка основной теоремы алгебры и теоремы о разложерациональной дроби
4)
Для интегрирования рациональной
функции ![]() ,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
Для интегрирования рациональной функции , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:
Рассмотрим указанные шаги более подробно. Шаг 1. Преобразование неправильной рациональной дроби Если дробь неправильная (т.е. степень числителя P(x) больше степени знаменателя Q(x)), разделим многочленP(x) на Q(x). Получим следующее выражение:
где - правильная рациональная дробь. Шаг 2. Разложение знаменателя на простейшие дроби Запишем многочлен знаменателя Q(x) в виде
где квадратичные функции являются несократимыми, то есть не имеющими действительных корней. Шаг 3. Разложение рациональной дроби на сумму простейших дробей. Запишем рациональную функцию в следующем виде:
Общее число неопределенных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , ... должно быть равно степени знаменателя Q(x). Затем умножим обе части полученного уравнения на знаменатель Q(x) и приравняем коэффициенты при слагаемых с одинаковыми степенями x. В результате мы получим систему линейных уравнений относительно неизвестных коэффициентов Ai , Bi , Ki , Li , Mi , Ni , .... Данная система всегда имеет единственное решение. Описанный алгоритм представляет собой метод неопределенных коэффициентов. Шаг 4. Интегрирование простейших рациональных дробей. Простейшие дроби, полученные при разложении произвольной правильной рациональной дроби, интегрируются с помощью следующих шести формул:
У дробей с квадратичным знаменателем сначала необходимо выделить полный квадрат:
где
Интеграл
|
Пример 1 |
|
Вычислить
интеграл |
5.
Рациональные дроби. Простейшие рациональные дроби и их интегрирование
Как мы увидим ниже, далеко не всякая элементарная функция имеет интеграл, выражающийся в элементарных функциях. Поэтому очень важно выделить такие классы функций , интегралы которых выражаются через элементарные функции. Простейшим из этих классов является класс рациональных функций.
Всякую рациональную функцию можно представить в виде рациональной дроби, т. е. в виде отношения двух многочленов:

Не ограничивая общности рассуждения, будем предполагать, что эти многочлены не имеют общих корней.
Если степень числителя ниже степени знаменателя, то дробь называется правильной, в противном случае дробь называется неправильной.
Если дробь неправильная, то, разделив числитель на знаменатель (по правилу деления многочленов), можно представить данную дробь в виде суммы многочлена и некоторой правильной дроби:
 ;
;
здесь
М(х)-многочлен, а
 -
правильная дробь.
-
правильная дробь.
Пример. Пусть дана неправильная рациональная дробь

Разделив числитель на знаменатель (по правилу деления многочленов), получим
 .
.
Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных рациональных дробей.
Определение. Правильные рациональные дроби вида
(1).

(2).
 (k-целое
положительное число
(k-целое
положительное число
(3)
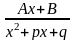 (корни знаменателя комплексные, т.е.
(корни знаменателя комплексные, т.е.
 ).
).
(4)
 (k-целое
положительное число
;корни
знаменателя комплексные), называются
простейшими дробями (1),(2),(3) и (4) типов.
(k-целое
положительное число
;корни
знаменателя комплексные), называются
простейшими дробями (1),(2),(3) и (4) типов.
Интегрирование простейших дробей типа (1),(2) и (3) не составляет большой трудности, поэтому мы приведем их интегрирование без каких-либо дополнительных пояснений:
(1)
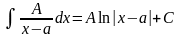
(2)

(3)

=
Более сложных вычислений требует интегрирование простейших дробей (4) типа. Пусть нам дан интеграл такого типа:
(4)

Произведем преобразования:

Первый
интеграл берется подстановкой
 :
:

Второй интеграл- обозначим его через Ik-запишем в виде
 ,
,
полагая

(по
предположению корни знаменателя
комплексные, а следовательно,
 ).
Далее поступаем следующим образом:
).
Далее поступаем следующим образом:
 .
.
Преобразуем интеграл:

Интегрируя по частям ,будем иметь
 .
.
Подставляя это выражение в равенство (1), получим

=
=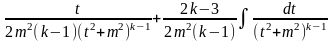 .
.
В
правой части содержится интеграл того
же типа, что
 ,
но показатель степени знаменателя
подынтегральной функции на единицу
ниже
,
но показатель степени знаменателя
подынтегральной функции на единицу
ниже
 ;таким
образом, мы выразили
через
;таким
образом, мы выразили
через
 Продолжая
идти тем же путем, дойдем до известного
интеграла:
Продолжая
идти тем же путем, дойдем до известного
интеграла:

Подставляя затем всюду вместо t и m их значения, получим выражение интеграла (4) через х и заданные числа А, B, p,q.
Интегрирование рациональных дробей
Пусть
требуется вычислить интеграл от
рациональной дроби
 Если
данная дробь неправильная, то мы
представляем ее в виде суммы многочлена
M(x) и правильной рациональной дроби
.
Последнюю же представляем по формуле
в виде суммы простейших дробей. Таким
образом, интегрирование всякой
рациональной дроби сводится к
интегрированию многочлена и нескольких
простейших дробей.
Если
данная дробь неправильная, то мы
представляем ее в виде суммы многочлена
M(x) и правильной рациональной дроби
.
Последнюю же представляем по формуле
в виде суммы простейших дробей. Таким
образом, интегрирование всякой
рациональной дроби сводится к
интегрированию многочлена и нескольких
простейших дробей.
Вид простейших дробей определяется корнями знаменателя f(x). Здесь возможны следующие случаи.
1.Случай.
Корни знаменателя действительны и различны, т. е.
F(x)=(x-a)(x-b)…(x-d).
В этом случае дробь разлагается на простейшие дроби 1типа:

и тогда

2. Случай.
Корни знаменателя действительные, причем некоторые из них кратные:
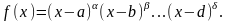
В этом случае дробь разлагается на простейшие дроби 1и 2 типов.
Пример 1.
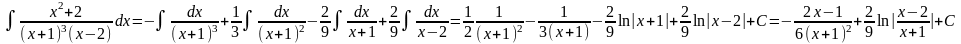
3. Случай.
Среди корней знаменателя есть комплексные неповторяющиеся(т.е. различные):

В этом случае дробь разлагается на простейшие дроби 1,2 и 3 типов.
Пример 2.Требуется вычислить интеграл
 .Разложим
подынтегральную дробь на простейшие:
.Разложим
подынтегральную дробь на простейшие:
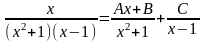
Следовательно,
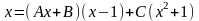 .
.
Полагая х=1, получим 1=2С, С= ½; полагая х=0, получим 0= -B+C, B=1/2.
Приравнивая
коэффициенты при
 ,
получим 0=А+С, откуда А= - ½. Таким образом
,
,
получим 0=А+С, откуда А= - ½. Таким образом
,
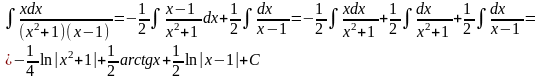
4. Случай.
Среди корней знаменателя есть комплексные кратные:

В этом случае разложение дроби будет содержать и простейшие дроби 4 типа.
Пример 3. Требуется вычислить интеграл
 .
.
Решение. Разлагаем дробь на простейшие:
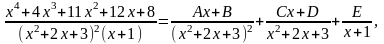
откуда

Комбинируя указанные выше методы определения коэффициентов, находим А=1, В= - 1, С=0, D=0, Е=1.
Таким образом, получаем
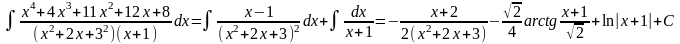
Из всего изложенного следует, что интеграл от любой рациональной функции может быть выражен через элементарные функции в конечном виде, а именно:
через логарифмы- в случаях простейших дробей 1 типа;
через рациональные функции- в случае простейших дробей 2 типа
через логарифмы и арктангенсы- в случае простейших дробей 3 типа
через рациональные функции и арктангенсы- в случае простейших дробей 4 типа.
6)
Задачи, приводящие к понятию определённого
интеграла

Геометрический смысл определённого интеграла (площадь криволинейной трапеции) |
S
–
площадь криволинейной трапеции,
ограниченной сверху графиком функции
y
= f(x) снизу – осью ОХ, слева – вертикальной прямой х = а, справа – вертикальной прямой х = b.
|
Физический
смысл определённого
интеграла (работа переменной силы,
путь при неравномерном движении точки,
масса неоднородного стержня) |
1.
2.
Путь
при
этом равен:
3.
Масса
m
такого
стержня равна:
|
7)
Определение определённого интеграла
|
Функция
f(x)
называется интегрируемой
(по Риману)
на промежутке
[a,
b],
если существует
При
этом число
[a, b] и обозначается так: |
Продолжение 6 вопрос.
8)смотри 7. § Условия интегрируемости функций (классы интегрируемых функций)
Теорема (необходимое условие) |
Пусть функция f(x) интегрируема на промежутке [a, b]. Тогда она ограничена на этом промежутке. |
Примеры.
1.

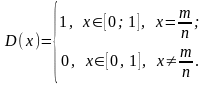 2.
Функция Дирихле
2.
Функция Дирихле
Теорема (1-е достаточное условие) |
Непрерывная на замкнутом промежутке [a, b] функция f(x) интегрируема на этом промежутке. |
Следствие |
Всякая элементарная функция интегрируема на любом промежутке, целиком лежащем в области определения этой функции (так как она непрерывна на этом промежутке). |
Теорема (2-е достаточное условие) |
Кусочно непрерывная функция (т. е. имеющая на промежутке [a, b] конечное число точек разрыва I рода) интегрируема на этом промежутке. |
Теорема (3-е достаточное условие) |
Монотонная ограниченная на промежутке [a, b] функция интегрируема на этом промежутке. |
Классы интегрируемых функций (формулировки теорем о достаточных условиях интегрируемости функций). Что Вы можете сказать на основании известных Вам теорем о необходимых и достаточных условиях об интегрируемости следующих функций…?
Необходимое условие интегрируемости функции
Если функция f (x) интегрируема на отрезке [a, b], то она ограничена на этом отрезке. Доказательство. Предположим обратное. Допустим, что f (x) является неограниченной на отрезке [a, b]. Покажем, что в этом случае интегральную сумму можно сделать сколь угодно большой за счет выбора точек ξ 1, ξ 2,…, ξ n при любом разбиении отрезка [a, b]. Действительно, так как f (x) не ограничена на [a, b], то при любом разбиении отрезка [a, b] она обладает этим свойством хотя бы на одном частичном отрезке разбиения, например на [x0, x1]. Выберем на остальных частях отрезка точки ξ 2, ξ 3,…, ξ n произвольно и обозначим
![]()
Зададим произвольное число М > 0 и возьмем такое ξ 1 на [x0, x1], чтобы
 .
.
Это можно сделать в силу неограниченности функции f (x) на [x0, x1]. Тогда
![]() и
и ![]() ,
,
т.е. интегральная сумма σ по абсолютной величине может быть больше любого наперед заданного числа. Поэтому интегральная сумма σ не имеет конечного предела при λ → 0, а это означает, что определенный интеграл от неограниченной функции не существует. Замечание. Обратная теорема неверна, т.е. условие ограниченности функции f (x) необходимое, но не является достаточным условием интегрируемости функции. Поясним это утверждение примером. Рассмотрим функцию Дирихле на отрезке [0,1]:
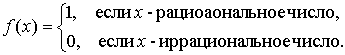
Функция Дирихле, очевидно, ограниченна. Однако она не интегрируема на [0,1]. Действительно, если при любом разбиении отрезка [0,1] выбрать рациональные точки ξ i (x i - 1 ≤ ξ i ≤ x i ), то получим
 ,
,
а если взять ξ i иррациональным, то получим
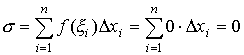 .
.
Таким образом, при разбиении на сколь угодно малые частичные отрезки интегральная сумма может принимать как значение, равное 0, так и значение, равное 1. Поэтому интегральная сумма σ при λ → 0 предела не имеет. Для существования определенного интеграла от некоторой функции f (x) последняя, помимо ограниченности, должна обладать дополнительными свойствами, обеспечивающими ее интегрируемость. Для установления этих свойств необходимо ввести понятия нижних и верхних сумм.



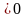 ,
,



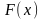 − сила, параллельная оси 0Х
и
ориентированная в положительном
направлении оси 0Х,
действующая на материальную точку
при прямолинейном перемещении по
промежутку [a,
b].
Работа А
силы
при
этом равна:
− сила, параллельная оси 0Х
и
ориентированная в положительном
направлении оси 0Х,
действующая на материальную точку
при прямолинейном перемещении по
промежутку [a,
b].
Работа А
силы
при
этом равна:
 .
. − скорость неравномерного прямолинейного
движения материальной точки.
− скорость неравномерного прямолинейного
движения материальной точки.
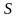 ,
пройденный точкой за промежуток
времени
,
пройденный точкой за промежуток
времени
 ,
,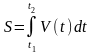 .
. − плотность неоднородного прямолинейного
стержня с концами в точках
− плотность неоднородного прямолинейного
стержня с концами в точках
 .
.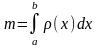 .
.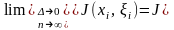 .
. называется определенным
интегралом от
функции f(x)
по промежутку
называется определенным
интегралом от
функции f(x)
по промежутку