11. Дисперсия, ее свойства.

Дисперсия ( ) - средняя из квадратов отклоне­ний вариантов значений признака от их средней величины:

Или   для не сгруппированных данных,

 для сгруппированных данных.

Свойства дисперсии.

1. Дисперсия постоянной величины равна 0.

2. Уменьшение всех значений признака на одну и ту же величину не изменяет величину дисперсии:

3. Уменьшение всех значений признака в к раз уменьшает дисперсию в k² раз: 

4. Средний квадрат отклонений, исчисленный от среднего арифметического, всегда будет меньше среднего квадрата отклонений, исчисляемого от любой другой величины:  >  . Величина различия между ними вполне определенная, это квадрат разности между средней и этой условной величиной А.

, , .

12. Правило сложения дисперсий. Коэффициент детерминации и эмпирическое корреляционное отношение.

Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий.

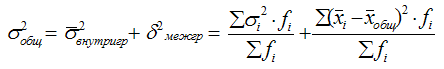
Эмпирический коэффициент детерминации широко используется в задачах статистики и является показателем, который представляет долюмежгруппопой дисперсии в общей дисперсии результативного признака и характеризует силу влияния группировочного признака на образование общей вариации. Он может быть рассчитан по формуле:

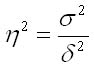
Данный коэффициент показывает долю вариации результативного признака у под влиянием фактора х. При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной сильной связи — единице.

Эмпирическое корреляционное отношение представляется как корень квадратный из эмпирического коэффициента детерминации. Оно показывает тесноту связи между статистическими данными и определяется по формуле:

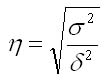
где числитель — дисперсия групповых средних; знаменатель — общая дисперсия.

Корреляционное отношение равно нулю, если связи между данными нет. В таком случае все групповые средние будут равны между собой и межгрупповой вариации не будет.

Корреляционное отношение равно единице тогда, когда связь функциональная. В этом случае дисперсия групповых средних будет равна общей дисперсии, т. е. внутригрупповой вариации не будет.

Чем значения корреляционного отношения ближе к единице, тем сильнее, ближе к функциональной зависимости связь между признаками.

13. Среднее значение и вариация альтернативного признака.

Среднее значение альтернативного признака и его дисперсия:

1. Среднее значение альтернативного признака

2. Дисперсия альтернативного признака

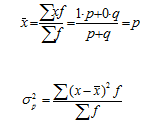
Подставив в формулу дисперсии q = 1 – p, получим:

Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным признаком и доли единиц, не обладающих данным признаком.

Среднее квадратическое отклонение альтернативного признака:

Вариация альтернативного признака заключается в наличии или отсутствии изучаемого свойства у единиц совокупности. Количественно вариация альтернативного признака выражается двумя значениями: наличие у единицы изучаемого свойства обозначается единицей (1), а его отсутствие — нулем (0). Долю единиц, обладающих изучаемым признаком, обозначают буквой  , а долю единиц, не обладающих этим признаком — через  . Учитывая, что p + q = 1 (отсюда q = 1 — p), а среднее значение альтернативного признака равно 

,

средний квадрат отклонений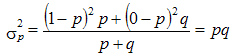

Таким образом, дисперсия альтернативного признака равна произведению доли единиц, обладающих данным свойством ( ), на долю единиц, данным свойством не обладающих ( ).

Максимальное значение средний квадрат отклонения (дисперсия) принимает в случае равенства долей, т.е. когда   т.е.  . Нижняя граница этого показателя равна нулю, что соответствует ситуации, при которой в совокупности отсутствует вариация. Среднее квадратическое отклонение альтернативного признака: