Лекции по алгебре и геометрии. Лекция 29. Теория линейных операторов.

Краткое содержание: собственные числа и собственные векторы линейного оператора. Диагонализируемость линейного оператора. Матрица как линейный оператор. Собственное подпространство. Характеристический многочлен. Признаки диагонализируемости матрицы (линейного оператора).

П.1. Собственные числа и собственные векторы линейного оператора.

Пусть – линейный оператор, определенный на векторном пространстве V над полем K.

Определение. Ненулевой вектор называется собственным вектором линейного оператора f, если существует скаляр такой, что

.

Этот скаляр называется собственным числом (собственным значением) линейного оператора f, отвечающим собственному вектору х. Собственный вектор х называется также собственным вектором, отвечающим собственному числу .

Определение. Линейный оператор называется диагонализируемым, если существует базис векторного пространства V, относительно которого его матрица является диагональной.

Теорема. (Первый необходимый и достаточный признак диагонализируемости линейного оператора.)

Для того, чтобы линейный оператор был диагонализируемым, необходимо и достаточно, чтобы существовал базис из его собственных векторов.

Доказательство. Пусть линейный оператор является диагонализируемым. Тогда, по определению, существует базис векторного пространства V, относительно которого матрица А линейного оператора f является диагональной. По определению матрицы линейного оператора относительно базиса имеют место равенства

.

Координаты вектора относительно базиса образуют i-й столбец матрицы А:

.

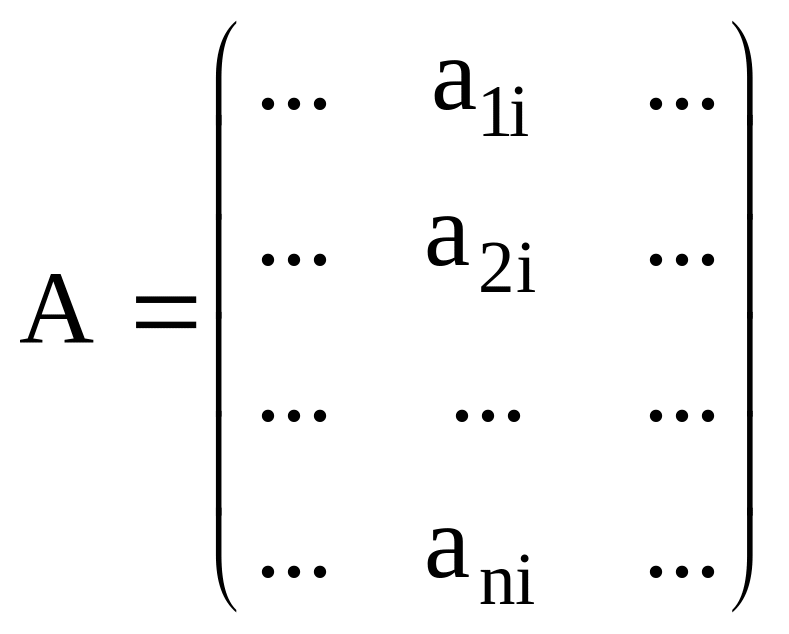Так как А является диагональной, то все элементы i-го столбца равны нулю, кроме элемента для всех . Отсюда следует, что выполняются равенства:

.

Так как базисный вектор, то он отличен от нулевого и, следовательно, является собственным вектором линейного оператора f для всех . Тем самым мы доказали существование базиса из собственных векторов.

Пусть теперь, базис из собственных векторов линейного оператора f. По определению, для каждого вектора , , существует скаляр

, такой, что . Из определения матрицы линейного оператора относительно базиса , из этих равенств следует, что матрица А линейного оператора f является диагональной:

.

.

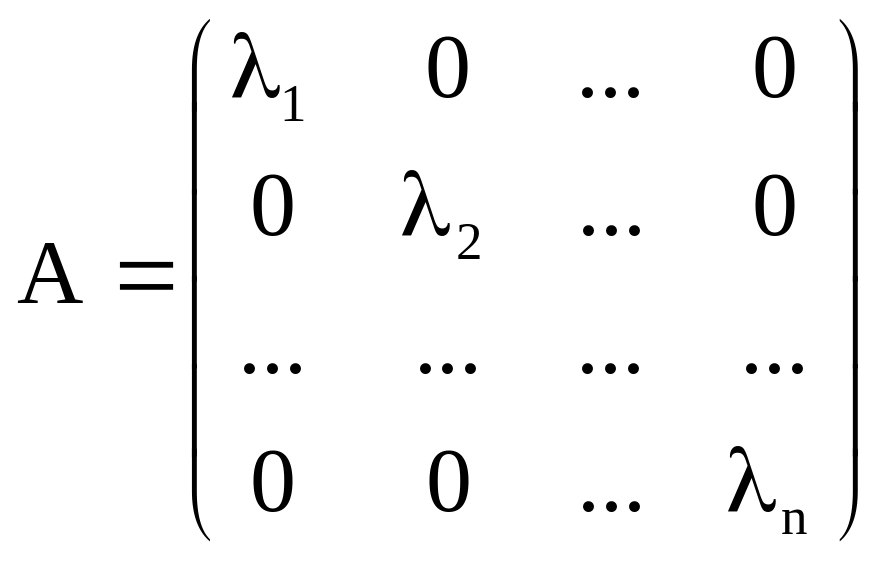Теорема доказана.

Следствие. Матрица линейного оператора f относительно базиса является диагональной:

тогда и только тогда, когда – базис из собственных векторов линейного оператора f, а диагональные элементы матрицы А являются его собственными числами.

П.2. Собственное подпространство.

Всюду, далее, мы будем полагать, что векторное пространство V является пространством столбцов высоты n над полем K: . Любой линейный оператор задается в этом пространстве с помощью матрицы, причем оператор и его матрица будут для нас синонимами и обозначаться будут одной и той же буквой:

, , ,

причем матрица А является матрицей линейного оператора А относительно канонического базиса пространства .

Собственные числа и собственные векторы линейного оператора А мы будем называть собственными числами и собственными векторами матрицы А. Дадим строгое определение.

Определение. Ненулевой столбец называется собственным вектором матрицы , отвечающим собственному числу , если

.

Этот скаляр называется собственным числом матрицы А, отвечающим собственному вектору Х.

Определение. Матрица называется диагонализируемой над полем K, если соответствующиий ей линейный оператор А является диагонализируемым, т.е. если существует базис пространства , относительно которого матрица линейного оператора А является диагональной.

Соответственно формулируется 1-й необходимый и достаточный признак диагонализируемости матрицы А.

Теорема. (Первый необходимый и достаточный признак диагонализируемости матрицы.) Матрица диагонализируема над полем K тогда и только тогда, когда существует базис пространства из собственных векторов матрицы А.

Обозначение. Обозначим через множество всех собственных векторов матрицы А, отвечающие одному и тому же собственному числу , и включим в это множество нулевой вектор, т.е.

.

Теорема. , где Е – единичная матрица.

Доказательство. Равенство равносильно равенству или . Отсюда следует, что

.

Теорема доказана.

Следствие. Множество всех собственных векторов матрицы А, отвечающие данному собственному числу совпадает с множеством решений однородной системы линейных уравнений , и является векторным подпространством пространства столбцов .

Определение. Подпространство называется собственным подпространством, отвечающим собственному числу .

Теорема (о необходимых и достаточных признаках собственного числа матрицы). Следующие условия равносильны:

1) – собственное число матрицы А;

2) ;

3) .

Доказательство. . Пусть – собственное число матрицы А, тогда существует ненулевой столбец такой, что . Отсюда следует, что Х есть ненулевое решение однородной системы линейных уравнений , т.е. , откуда следует что ядро матрицы является ненулевым, ч.т.д.

. Пусть . Отсюда следует, что , т.е. , где n – порядок матрицы . Отсюда следует, что , ч.т.д.

. Пусть , тогда система имеет нетривиальное решение Х (почему?), откуда следует, что , т.е. Х является собственным вектором, а – собственным числом матрицы А, ч.т.д.

Теорема доказана.