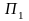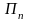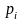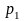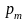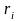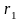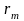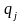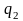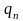42. Игры с природой. Специфика игр с природой.

Игры с природой образуют специальный класс матричных игр, в которых одним из участников является человек или группа лиц, объединенных общностью цели (игрок А), а другим – «природа» (игрок П). Под термином «природа» подразумевается весь комплекс внешних условий, при которых игроку А приходится принимать решение. Природа безразлична к выигрышу и не стремится обратить в свою пользу промахи игрока А.

Игрок А может использовать т стратегий А₁,А₂,…,А_т, а природа может реализовать п различных состояний П₁,П₂,…,П_п. Игроку А могут быть известны вероятности q_j, с которыми природа реализует свои состояния П_j. Действуя против природы, игрок А может пользоваться как чистыми А_i, так и смешанными стратегиями. Если он имеет возможность численно оценить (величиной а_ij) последствия применения каждой своей чистой стратегии А_i при любом состоянии П_j природы, то игру можно задать платежной матрицей.

			…
			…
			…
…	…	…	…	…	…
			…
			…

При упрощении платежной матрицы игры с природой имеется своя специфика: отбрасывать те или иные состояния природы нельзя, так как она может реализовать любое состояние не зависимо от того, выгодно оно или нет.

При выборе оптимальной стратегии игрока А пользуются различными критериями. При этом опираются как на платежную матрицу, так и на матрицу рисков.

Риском r_ij игрока А, когда он пользуется чистой стратегией А_i при состоянии П_j природы, называется разность между максимальным выигрышем 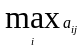, который он мог бы получить, если бы достоверно знал, что природой будет реализовано именно состояние П_j, и тем выигрышем, который он получит, используя стратегию А_i, не зная какое же состояние природа реализует. Таким образом, элементы матрицы рисков определяются по формуле 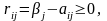где - максимально возможный выигрыш игрока А при состоянии П_j

			…
			…
			…
…	…	…	…	…	…
			…
			…

42. Критерий Байеса

Если вероятности q_j состояний природы известны, то пользуются критериями Байеса и Лапласа.

В качестве оптимальной по критерию Байеса принимается чистая стратегия А_i, при которой максимизируется средний выигрыш 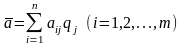игрока А.

42. Критерий Лапласа.

Если игроку А представляются в равной мере правдоподобными все состояния природы, то 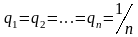и оптимальной по критерию Лапласа считается чистая стратегия А_i, обеспечивающая .

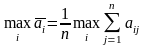42. Критерий Вальда.

Оптимальной по критерию Вальда считается чистая стратегия А_i, при которой наименьший выигрыш 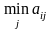игрока А будет максимальным.

42. Критерий Сэвиджа.

Оптимальной по критерию Сэвиджа считается та чистая стратегия А_i, при которой минимизируется величина максимального риска, т.е. обеспечивается .

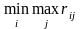42. Критерий Гурвица.

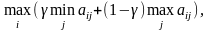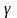Оптимальной по критерию Гурвица считается чистая стратегия А_i, найденная из условия где принадлежит интервалу (0,1) и выбирается из субъективных соображений.