
- •1(1) Колебания. Возвращающая сила. Устойчивое и неустойчивое равновесие.
- •1(2) Колебания. Возвращающая сила. Устойчивое и неустойчивое равновесие.
- •2.(1) Пружинный маятник. Дифференциальное уравнение гармонических колебаний и его решение.
- •2.(2) Пружинный маятник. Дифференциальное уравнение гармонических колебаний и его решение.
- •3(1). Физический и математический маятники
- •5.Идеальный колебательный контур.
- •6 Энергия гармонического осциллятора
- •13(1).Дифференциальное уравнение затухающих механических колебаний и его решение.
- •13(2).Дифференциальное уравнение затухающих механических колебаний и его решение.
- •14.Энергия затухающего осциллятора.
- •15.Добротность гармонического осциллятора с затуханием.
- •16.(1) Затухающие гармонические колебания в электрическом контуре.
- •16.(2) Затухающие гармонические колебания в электрическом контуре.
- •17.Вынужденные электрические колебания.
- •18.Импеданс электрического колебательного контура.
- •20.Мощность, выделяющаяся в цепи переменного тока.
- •21(2) Вынужденные колебания
- •Волновые процессы. Уравнение волны.
- •2.Электромагнитные волны(интенс., поляр., об. Пл. Энергии,). Шкала э.-м. Волн. Кривая чувствительности глаза.
- •3,Плоские волны в упругой среде.
- •4,Отражение и преломление э.-м. Волн.
- •5,Бегущие гармонические волны, их характеристики
- •6,Эффект Доплера
- •8. Перенос энергии электромагнитной волной.
- •9. Излучение диполя.
- •10. Перенос энергии звуковой волной.
- •11. Стоячие волны.
- •12 Продольные и поперечные волны.Поляризация
- •13. Шкала электромагнитных волн
- •14(1). Принцип суперпозиции волн. Условия когерентности. Интерфе-ренция.
- •14(1). Принцип суперпозиции волн. Условия когерентности. Интерфе-ренция.
- •17. Способы получения когерентных световых волн.
- •18.(2) Принцип Гюйгенса
- •19. Дифракция Френеля на круглом отверстии
- •20. Дифракция на круглом диске. Зонная пластинка.
- •21(1). Дифракция Фраунгофера на щели
- •21.(2) Дифракция Фраунгофера на щели
- •22.Дифракция на одномерной решётке.
- •23. Зависимость дифракционной картины от параметров решетки. Спектральные приборы.
- •24 Дифракция на пространственной решетке
- •25. Зависимость показателя преломления от частоты излучения. Дисперсия.
- •26. Поглощение электромагнитной волны веществом. Закон Бугера.
- •27. Фазовая и групповая скорости волны.
- •28.Поляризация света
- •29. Закон Малюса.
- •30. Закон Брюстера.
- •31 (1)Рассеяние света.
- •31 (2)Рассеяние света.
- •32.(2) Тепловое излучение
- •33. Спектральная плотность энергетической светимости.
- •34.Закон Кирхгофа и следствие из него.
- •35 Черные и серые тела.
- •37.Законы теплового излучения. Закон Ст.-Больцмана.
- •40.(1)Формула Планка.
- •40.(2)Формула Планка.
- •41.Пирометрия.
24 Дифракция на пространственной решетке
Для
наблюдения дифракционной картины
необходимо, чтобы постоянная решетки
была того же порядка, что и длина волны
падающего излучения ![]() (m=0,
1, 2, ...) . Кристаллы, являясь трехмерными
пространственными решетками (см. §
Пространственная решетка. Рассеяние
света), имеют постоянную порядка 10 -10 м
и, следовательно, непригодны для
наблюдения дифракции в видимом свете
(
(m=0,
1, 2, ...) . Кристаллы, являясь трехмерными
пространственными решетками (см. §
Пространственная решетка. Рассеяние
света), имеют постоянную порядка 10 -10 м
и, следовательно, непригодны для
наблюдения дифракции в видимом свете
(![]() м).
Эти факты позволили немецкому физику
М. Лауэ (1879-1960) прийти к выводу, что в
качестве естественных дифракционных
решеток для рентгеновского излучения
можно использовать кристаллы, поскольку
расстояние между атомами в кристаллах
одного порядка с
м).
Эти факты позволили немецкому физику
М. Лауэ (1879-1960) прийти к выводу, что в
качестве естественных дифракционных
решеток для рентгеновского излучения
можно использовать кристаллы, поскольку
расстояние между атомами в кристаллах
одного порядка с ![]() рентгеновского
излучения (
рентгеновского
излучения (![]() м).
м).
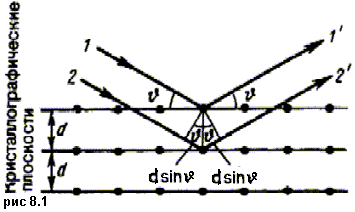
Простой метод расчета дифракции рентгеновского излучения от кристаллической решетки предложен независимо друг от друга Г. В. Вульфом (1863-1925) и английскими физиками Г. и Л. Брэггами (отец (1862-1942) и сын (1890-1971)). Они предположили, что дифракция рентгеновского излучения является результатом его отражения от системы параллельных кристаллографических плоскостей (плоскостей, в которых лежат узлы (атомы) кристаллической решетки).
Представим
кристаллы в виде совокупности параллельных
кристаллографических плоскостей (рис.
8.1), отстоящих друг от друга на расстоянии
d. Пучок параллельных монохроматических
рентгеновских лучей (1, 2) падает под
углом скольжения ![]() (угол
между направлением падающих лучей и
кристаллографической плоскостью) и
возбуждает атомы кристаллической
решетки, которые становятся источниками
когерентных вторичных волн 1' и 2',
интерферирующих между собой, подобно
вторичным волнам, от щелей дифракционной
решетки. Максимумы интенсивности
(дифракционные максимумы) наблюдаются
в тех направлениях, в которых все
отраженные атомными плоскостями волны
будут находиться в одинаковой фазе.
Эти направления удовлетворяют формуле
Вульфа - Брэггов
(угол
между направлением падающих лучей и
кристаллографической плоскостью) и
возбуждает атомы кристаллической
решетки, которые становятся источниками
когерентных вторичных волн 1' и 2',
интерферирующих между собой, подобно
вторичным волнам, от щелей дифракционной
решетки. Максимумы интенсивности
(дифракционные максимумы) наблюдаются
в тех направлениях, в которых все
отраженные атомными плоскостями волны
будут находиться в одинаковой фазе.
Эти направления удовлетворяют формуле
Вульфа - Брэггов
![]() (m-1,2,3,
...), (8.1)
(m-1,2,3,
...), (8.1)
т. е. при разности хода между двумя лучами, отраженными от соседних кристаллографических плоскостей, кратной целому числу длин волн , наблюдается дифракционный максимум.
При произвольном направлении падения монохроматического рентгеновского излучения на кристалл дифракция не возникает. Чтобы ее наблюдать, надо, поворачивая кристалл, найти угол скольжения. Дифракционная картина может быть получена и при произвольном положении кристалла, для чего нужно пользоваться непрерывным рентгеновским спектром, испускаемым рентгеновской трубкой. Тогда для таких условий опыта всегда найдутся длины волн , удовлетворяющие условию (8.1).
Рентгенострукту́рный ана́лиз (рентгенодифракционный анализ) — один из дифракционных методов исследования структуры вещества. В основе данного метода лежит явлениедифракции рентгеновских лучей на трехмерной кристаллической решётке.
Явление дифракции рентгеновских лучей на кристаллах открыл Лауэ, теоретическое обоснование явлению дали Вульф и Брэгг (условие Вульфа-Брэгга
РЕНТГЕ́НОВСКАЯ СПЕКТРОСКОПИ́Я, методы исследования атомной структуры по рентгеновским спектрам. Для получения рентгеновских спектров исследуемое вещество бомбардируют электронами в рентгеновской трубке либо возбуждают флуоресценцию исследуемого вещества, облучая его рентгеновским излучением.
