17. Способы получения когерентных световых волн.

Для получения когерентных световых волн применяют метод разделения волны, излучаемой одним источником, на две части, которые после прохождения разных оптических путей накладываются друг на друга, и наблюдается интерференционная картина.

Пусть разделение на две когерентные волны происходит в определенной точке О. До точки M, в которой наблюдается интерференционная картина, одна волна в среде с показателем преломления п1 прошла путь s1, вторая — в среде с показателем преломления n2 — путь s2. Если в точке О фаза колебаний равна wt, то в точке М первая волна возбудит колебание A1cos(t–s1/v1), вторая волна — колебание A2cos(t–s2/v2), где v1=c/n1, v2=c/n2 — соответственно фазовая скорость первой и второй волны. Разность фаз колебаний, возбуждаемых волнами в точке М, равна

(учли, что w /с = 2pn/с = 2p/l0, где l0 — длина волны в вакууме). Произведение геометрической длины s пути световой волны в данной среде на показатель n преломления этой среды называется оптической длиной пути L, a D = L2 – L1 — разность оптических длин проходимых волнами путей — называется оптической разностью хода. Если оптическая разность хода равна целому числу длин волн в вакууме

  (172.2)

то d = ±2тp, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в одинаковой фазе. Следовательно, (172.2) является условием интерференционного максимума.

Если оптическая разность хода

  (172.3)

то d = ±2(т+1)p, и колебания, возбуждаемые в точке М обеими волнами, будут происходить в противофазе. Следовательно, (172.3) является условием интерференционного минимума.

18.(1) Принцип Гюйгенса — Френеля: Каждый элемент волнового фронта можно рассматривать как центр вторичного возмущения, порождающего вторичные сферические волны, а результирующее световое поле в каждой точке пространства будет определяться интерференцией этих волн.

Д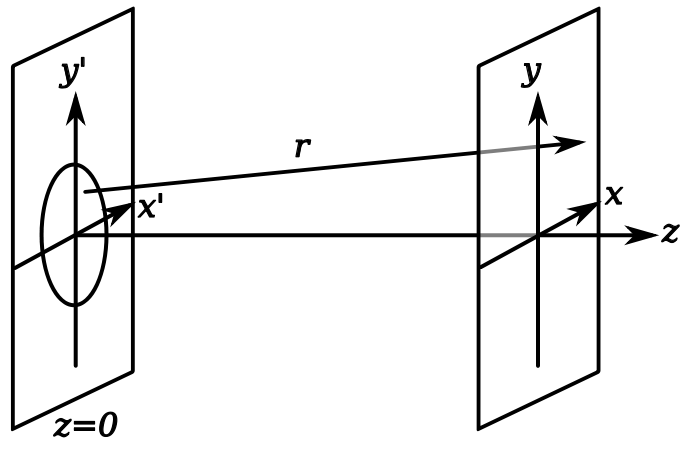 ифракция Френеля:

На рисунке изображён непрозрачный экран с круглым отверстием, на некотором расстоянии от которого расположен источник света. Изображение фиксируется на другом экране справа. Вследствие дифракции свет, проходящий через отверстие, расходится. Поэтому область, которая была затенена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец.

Дифракция Фраунгофера:

Случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Метод зон Френеля: