
- •Понятие вектора. Понятие прямого произведения множеств. Теорема о мощности прямого произведения множеств.
- •Понятие соответствия между множествами. Всюду определенное, сюръективное, функциональное, взаимно однозначное соответствие.
- •Счетное множество
- •Понятие отношения. Свойства отношений. Отношение эквивалентности, отношение строгого порядка, отношение нестрогого порядка.
- •Понятие операции, ассоциативной операции, дистрибутивной операции. Понятие алгебры, алгебраической системы, модели. Понятие группоида, полугруппы, коммутативной полугруппы.
- •Понятие композиции. Теорема о числе композиций n.
- •Понятие сильной связности. Анализ сильной связности с помощью алгоритмов поиска на графах.
- •Связность графа. Отыскание компонент связности при графическом задании графа.
- •Связность графа. Отыскание компонент связности при графическом задании графа.
- •Булева алгебра. Основные свойства операций булевой алгебры. Понятие двойственной и самодвойственной логической функции.
- •Двойственность. Принцип двойственности.
- •Разложение логической функции по переменным. Понятие совершенной дизъюнктивной нормальной формы логической функции. Понятие совершенной конъюнктивной нормальной формы логической функции.
- •Понятие полинома логической функции(полинома Жегалкина). Понятие линейной логической функции.
- •Второй этап(табличный) (получение минимальной формы)
- •Важнейшие замкнутые классы.
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО ДИСКРЕТНОЙ МАТЕМАТИКЕ
Основные понятия теории множеств. Понятие мультимножества. Способы задания множеств. Операции над множествами. Теорема о числе подмножеств n-элементного множества.
В
основе теории множеств лежат первичные
понятия: множество и
отношение быть
элементом множества
(обозначается как ![]() [3] —
«x есть элемент множества A», «x принадлежит
множеству A»). Среди производных понятий
наиболее важны следующие:
[3] —
«x есть элемент множества A», «x принадлежит
множеству A»). Среди производных понятий
наиболее важны следующие:
пустое множество, обычно обозначается символом
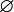 ;
;подмножество и надмножество;
семейство множеств;
пространство (Универсум);
конституента.
Операции над множествами.
1) объединение: множество тех элементов х, которые принадлежат хотя бы одному множеству. AB={x|xA или xB} 2) пересечение: общие элементы AB={x|xA и хВ}. 3) разность множеств.A\B={x|xA и xB} 4) симметрическая разность A_B={x|xA, то xB; xВ, то xA}.
Иногда бывает удобно все рассматриваемые множества в некоторой теории считать подмножествами некоторого одного множества, которое в этом случае зовут универсальным U. 5) A- дополнение множества А. Это есть U/A=A
Для множеств определены следующие бинарные отношения:
отношение равенства (обозначается как
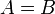 );
);отношение включения (обозначается как
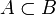 ).
).
Мультимножество — в математике, обобщение понятия множества, допускающее включение одного и того же элемента по нескольку раз.
Число элементов в мультимножестве, с учетом повторяющихся элементов, называется его размером или мощностью.
Любое подмножество конечного множества само конечно. Любое надмножество бесконечного множества само бесконечно.
Понятие вектора. Понятие прямого произведения множеств. Теорема о мощности прямого произведения множеств.
Вектором (кортежем) в линейной алгебре и дискретной математике называют упорядоченный набор элементов. Это не есть определение вектора, поскольку целесообразнее это понятие считать основным.
Элементы, определяющие
вектор, называются координатами или
компонентами. Координаты нумеруются
слева направо, а их число называется
длиной или размерностью вектора. В
отличие от элементов множества, координаты
вектора могут совпадать. Координаты
вектора заключаются в круглые скобки,
например
![]() .
Иногда скобки или запятые опускаются.
Часто векторы длины 2 называются
упорядоченными парами, длины 3 – тройками
и т. д.
.
Иногда скобки или запятые опускаются.
Часто векторы длины 2 называются
упорядоченными парами, длины 3 – тройками
и т. д.
Определение.
Два вектора равны, если они имеют равную
длину и их соответствующие координаты
равны. Иначе говоря, векторы
![]() и
и
![]() равны, если
равны, если
![]() и
и
![]() .
.
Определение.
Прямым произведением множеств А и В
(обозначение
![]() )
называется множество всех упорядоченных
пар
)
называется множество всех упорядоченных
пар
![]() ,
таких, что
,
таких, что
![]() .
В частности, если А=В, то обе координаты
принадлежат множеству А, такое произведение
обозначается А2.
Аналогично, прямым произведением
множеств
.
В частности, если А=В, то обе координаты
принадлежат множеству А, такое произведение
обозначается А2.
Аналогично, прямым произведением
множеств
![]() называется
множество всех векторов
длины
п,
таких, что
называется
множество всех векторов
длины
п,
таких, что
![]() .
.
Теорема 1.1.
Мощность
произведения конечных множеств
![]() равна произведению мощностей этих
множеств:
равна произведению мощностей этих
множеств:
![]() .
.
Понятие соответствия между множествами. Всюду определенное, сюръективное, функциональное, взаимно однозначное соответствие.
Определение.
Соответствием между множествами А и В
называется некоторое подмножество G
их декартова произведения:
![]() .
.
Если
![]() ,
то говорят, что
,
то говорят, что
![]() соответствует
соответствует
![]() при соответствии
при соответствии
![]() .
При этом множество всех таких
называют областью определения соответствия
.
При этом множество всех таких
называют областью определения соответствия
![]() ,
а множество соответствующих значений
называются областью значений соответствия
,
а множество соответствующих значений
называются областью значений соответствия
![]() .
.
В принятых
обозначениях, каждый элемент
![]() ,
соответствующий данному элементу
,
соответствующий данному элементу
![]() называется образом
при соответствии
,
наоборот, элемент
называется прообразом
элемента
при данном соответствии.
называется образом
при соответствии
,
наоборот, элемент
называется прообразом
элемента
при данном соответствии.
Соответствие
называется полностью
определённым,
если
![]() ,
то есть каждый элемент множества
,
то есть каждый элемент множества
![]() имеет хотя бы один образ во множестве
имеет хотя бы один образ во множестве
![]() ;
в противном случае соответствие
называется частичным.
;
в противном случае соответствие
называется частичным.
Соответствие
называется сюръективным,
если
![]() ,
то есть если каждому элементу множества
соответствует хотя бы один прообраз во
множестве
.
,
то есть если каждому элементу множества
соответствует хотя бы один прообраз во
множестве
.
Соответствие называется функциональным (однозначным), если любому элементу множества соответствует единственный элемент множества .
Соответствие называется инъективным, если оно является функциональным, и при этом каждый элемент множества имеет не более одного прообраза.
Соответствие называется взаимнооднозначным (биективным), если любому элементу множества соответствует единственный элемент множества , и наоборот. Можно сказать также, что соответствие является взаимнооднозначным, если оно является полностью определённым, сюръективным, функциональным, и при этом каждый элемент множества имеет единственный прообраз.
Понятие отображения множеств. Сюръективное, инъективное, биективное отображение.
Отображение: пусть имеем два множества Х и У. Отображением множества Х во множество У (пишем так: f: XY) называется f-правило, по которому каждому элементу х из Х ставится в соответствие единственный элемент у из У. y=f(x). Это отображение осуществляется с помощью функции y=f(x). У зовут образом Х, а Х зовут прообразом У. Если не для всех х из Х есть соответствие у из У, то это не отображение.
Свойство отображений:
1. f: xy зовут сюрьективным, если каждый элемент уÎУ обладает хоть одним прообразом. Если Х и У – конечные множества, то сюрьекцию можно осуществить, если мощность Х не меньше мощности У: |X|>=|Y|. Пример: является с. y=x3, не является – y=x2.
2. f: xy зовут инъективным, если каждый образ имеет ровно один прообраз. х1,х2 ÎХ, f(x1)=f(x2) => x1=x2. если множество конечно, то инъекция осуществима тогда, когда |X|<=|Y|. Пример: явл. и. – y=ex, не и. - y=x2, т.к. у(х)=у(-х).
Если отображение одновременно сюрьективно и инъективно, то его зовут биективным, или взаимно однозначным соответствием (пример: у=2х-3).
3. обратным отображением f—1 множества У во множество Х зовут множество таких х, что f(x)=y; f-1(y)={x|f(x)=y}. При обратном отображении образы и прообразы меняются местами => обратное отображение может осуществиться только тогда, когда отображение f: x®y биективное. (f-1)-1=f. Обратное отображение можно определить для инъекции, не являющейся сюрьекцией, но это будет частичным отображением, т.е. отображением, заданном на некотором подмножестве общего множества, которое в этом случае зовут областью определения отображения. Пример: f:y=ax, f-1:x=logay. Если у нас отображение сюрьективное, но не инъективное, то частичное обратное отображение построить нельзя.
Классификация множеств по мощности. Понятие счетного множества. Понятие несчётного множества.
