Вопрос 11 Вопрос 12 Зарядная мощность линии

Зарядная мощность линии не зависит от ее нагрузки. Реактивная индуктивная мощность, потребляемая линией, пропорциональна квадрату тока, протекающего по ней. При определенном значении нагрузки потребителей эти мощности станут равными, и так как зарядная мощность протекает навстречу реактивной индуктивной мощности, они взаимно скомпенсируются.

Из-за большой величины зарядной мощности линий сверхвысокого напряжения для дальних передач является обязательным применение поперечных реакторов, что является радикальным средством для снижения передачи реактивной мощности по линии и связанных с ней потерь энергии в режимах малых нагрузок. Мвар на передаваемый 1 МВт активной мощности.

Зарядная (емкостная) мощность трех фаз в конце линии:

–jQ^к_с12=3I^*к_с12U_2ф=

Необходимость учета емкости и зарядной мощности линии зависит от соиз-меряемости зарядной и нагрузочной мощности. В местных сетях небольшой протяженности при номинальных напряжениях до 35 кВ зарядные токи и мощности значительно меньше нагрузочных. Поэтому в КЛ емкостную проводимость учитывают только при напряжениях 20 и 35 кВ, а в ВЛ ею можно пренебречь

На величину реактивной мощности в электропередаче оказывает влияние зарядная мощность линии. Относительно небольшая зарядная мощность линий 110 - 220 кВ, в линиях напряжением 500 - 750 кВ большой протяженности она достигает весьма значительных величин, в результате чего выдача реактивной мощности от генераторов питающей станции в линию исключается, а избыточная реактивная мощность в линии компенсируется реакторами.

Вопрос 13 Расчет режима лэп при заданном токе нагрузки и напряжении в конце линии

Будем считать, что режим конца линии задан фазным напряжением U_ф=сonst и отстающим током нагрузки I₂. Также заданы Z₁₂=r₁₂+jx₁₂, в₁₂.

Необходимо определить:

1) напряжение в начале линии – U₁,

2) ток в продольной части – I₁₂,

3) потери мощности – DS₁₂,

4) ток в начале линии – I₁.

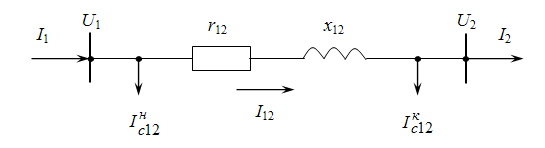
Расчет состоит в определении неизвестных токов и напряжений, последовательно от конца линии к началу.

Емкостный ток в конце линии 1-2, по закону Ома:

I^к_с12=U_2ф∙jв₁₂/2: (1)

 

Ток в продольной части линии 1-2, по первому закону Кирхгофа:

I₁₂=I₂+I^к_с12: (2)

Напряжение в начале линии по закону Ома:

U_1ф=U_2ф+I₁₂∙Z₁₂: (3)

Емкостный ток в начале линии:

I^н_с12=U_1ф∙jв₁₂/2: (4)

Ток в начале линии по первому закону Кирхгофа:

I₁=I₁₂+I^н_с12 (5)

Потери мощности в линии (в трех фазах):

DS₁₂=3I²₁₂∙Z₁₂: (6)

Векторная диаграмма токов и напряжений строится в соответствии с выражениями 1-5.

Вначале строим известные U_2ф и I₂.

Полагаем что U_2ф=U_2ф, т.е. напряжение U_2ф направлено по действительной оси. Емкостный ток I^к_с12опережает на 90^о напряжение U_2ф. Ток I₁₂ соединяет начало первого и конец второго суммируеммых векторов в правой части урав.(2) [I₁₂=I₂+ I^к_с12]

Затем строим отдельно два слагаемых в правой части (3) [U_1ф=U_2ф+I₁₂∙Z₁₂]. I₁₂∙Z₁₂=I₁₂∙r₁₂+I₁₂∙jx₁₂ (7)

Вектор I₁₂∙r₁₂ параллелен вектору I₁₂, вектор I₁₂∙jx₁₂ опережает на 90^о ток I₁₂

Напряжение U_1ф соединяет начало и конец суммируемых векторов U_2ф, I₁₂∙r₁₂, I₁₂∙jx₁₂.

Ток I^н_с12 опережает U_1ф на 90^о.

I₁ соответствует (5) I₁=I₁₂+I^н_с12

В линии с нагрузкой напряжение в конце линии по модулю меньше, чем в начале U_2ф<U_1ф.

На линии на холостом ходу (I₂=0), течет только емкостной ток, т.к. в соответствии с формулой I₁₂=I₂+I^к_с12 (2). I₁₂=I^к_с12

В этом случае напряжение в конце линии повышается U_2ф>U_1ф