4.7. Перенос теплоты теплопроводностью при стационарном режиме
Удельный тепловой поток через однородную плоскую стенку при стационарном режиме теплообмена (т. е. режиме передачи тепла, который не зависит от времени) определяется из соотношения
q = (tc1 – tc2)/Rλ, (4.30)
где tc1 и tc2 – температуры на поверхностях стенки, °С; Rλ = δ/λ – термическое сопротивление стенки, м2 град/ вт; δ – толщина стенки, м; λ – коэффициент теплопроводности стенки, вт/м град.
Для многослойной плоской стенки без учета термических сопротивлений контакта удельный тепловой поток при стационарном режиме будет:
q
= (tc1
– tc
(n+1))/
Rλi,
(4.31)
где tc1 и tc (n+1) – температуры на поверхностях стенок 1 и n +1, соответственно °С; Rλi = Rλ1+Rλ2+Rλ3+…+Rλn – сумма термических сопротивлений n стенок.
Уравнения (4.30) и (4.31) аналогичны закону Ома в электротехнике
I = U/R, (4.32)
где I – сила тока; U – напряжение; R – сопротивление проводника.
Задача № 5
Определить плотность теплового потока и рассчитать поле температур в плоской трехслойной стенке (рис. 4.2), состоящей из слоя штукатурки толщиной δш = 3 см, кирпича толщиной δк = 12 см и дерева толщиной δд = 6 см, если температура наружной поверхности штукатурки tc1 = –40 °С, а внутренней поверхности дерева tc2 = + 20 °С. Принять λш = 0,78 вт/м град, λк = 0,25 вт/м град, λд = 0,1 вт/м град. Построить график изменения температуры в стенке.
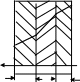
tc2
tc1
q
δш δк δд
Рис. 4.2
Решение
q = (tc2 – tc1)/(δш/ λш + δк/ λк + δд/ λд) = (20 + 40)/(0,03/0,78 + 0,12/0,25 + + 0,06/0,1) = 60/(0,03846 + 0,48 + 0,6) = 60/1,11846 = 53,645 вт/м2.
Определим t′с2 из уравнения:
q=(λд/ δд)(tc2 – t′с2 ).
То есть
t′с2 = tc2 – (q δд)/ λд = 20 – (53,645*0,06)/0,1 = 20 – 32,187 = –12,2 °C.
Из уравнения
q = (λк/ δк)(t′с2 – t′с1)
определим
t′с1 = t′с2 – (q δк)/ λк = –12,2 – (53,645*0,12)/0,25 = = –12,2 – 25,7 = –37,9 °C.
График изменения температуры в трехслойной стенке будет выглядеть следующим образом (рис. 4.3).
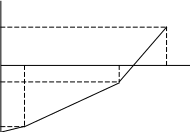
t °C
20
10
0
3 6 9 12 15 18 21 δ, см
– 10 –12,2 °С
– 20
– 30
– 37,9 °С
– 40
Рис. 4.3
Контрольная работа
В соответствии с учебным графиком студенты выполняют контрольную работу. Для правильного ее выполнения необходимо тщательно проработать соответствующие разделы дисциплины, указанные в рабочей программе и относящиеся к выполняемой работе. Вариант работы выбирается по порядковому номеру в журнале группы. Вариант должен быть указан на первом титульном листе работы.
Контрольную работу следует выполнять в отдельной тетради с полями не менее 3 см для заметок рецензента. Писать разборчиво и четко, не допускать перечеркиваний, вставок, произвольного сокращения слов и каких-либо обозначений, не принятых в литературе по изучаемой дисциплине.
Оформлять контрольную необходимо в соответствии с требованиями Единой системы конструкторской документации (ЕСКД), ГОСТ 2.105-68 «Основные требования к текстовым документам». Все расчеты должны быть выполнены в системе физических величин СИ, ГОСТ 9867-61.
Работа должна быть подписана студентом. В ней следует указать дату окончания выполнения работы.