40. Основные характеристики псевдоожиженного слоя.

Р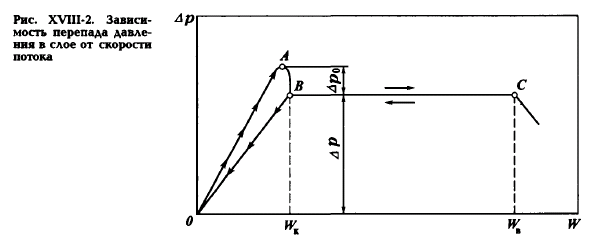 ис. XVIII-2. Зависимость перепада давления в слое

от скорости потока.

Для плотного и взвешенного слоев характерна

зависимость между скоростью ожижающего потока

и гидравлическим сопротивлением слоя. Левая

часть графика, представленная линиями ОА и

ОВ, соответствует движению ожижающего агента

через неподвижный слой, когда с увеличением

скорости потока сопротивление слоя растет. В точке

В сопротивление слоя оказывается равным его весу и

слой переходит во взвешенное

состояние; соответствующее этой точке значение

скорости называют критической скоростью W_К или скоростью начала псевдоожижения.

Перепад давления в точке А перед началом псевдоожижения превышает вес слоя на величину

«пика давления» ΔP₀, затрачиваемую потоком на преодоление сил сцепления между

частицами. Величина ΔP₀ зависит от плотности упаковки частиц, формы и состояния их

поверхности.

При дальнейшем увеличении скорости потока перепад давления в слое остается неизменным, и

линия «кривой псевдоожижения» идет параллельно оси абсцисс. Постоянство значения

перепада давления в слое (участок ВС) характеризуется равенством гидродинамического давления

и веса слоя,

приходящегося на единицу площади его поперечного сечения, и сохраняется до значения

W_В, соответствующего скорости витания, выше которой

частицы уносятся из слоя и наступает режим пневмотранспорта.

Перепад давления ΔР= H_og(ρ_Т-ρ)(l-ε₀),

где ρ_Т и ρ — соответственно плотность твердых частиц и потока.

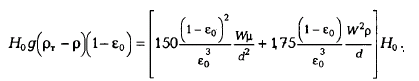
41. Основное уравнение гидростатики

Гидростатика - раздел гидравлики, в котором изучаются законы равновесия жидкостей. Важное место в гидростатике имеет понятие о гидравлическом давлении.

Выделим в жидкости, находящийся в равновесном состоянии, объем ∆V рис 1. Чтобы определить силы, действующие в жидкости, рассечем выделенный объем плоскостью ∆F, отбросим одну из частей, например верхнюю, и заменим действие отброшенной части силой ∆P.

Отношение ∆P к ∆F называется средним гидростатическим давлением

.

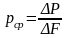
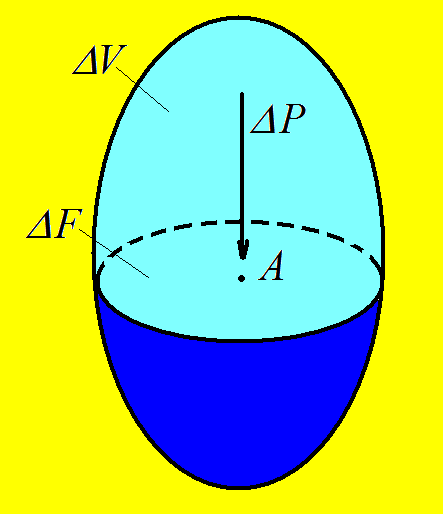Очевидно, что в каждой точке площадки ∆F гидростатическое давление будет различным, при этом среднее гидростатическое давление будет тем меньше отличаться от истинного, чем меньше величина площадки ∆F.

Р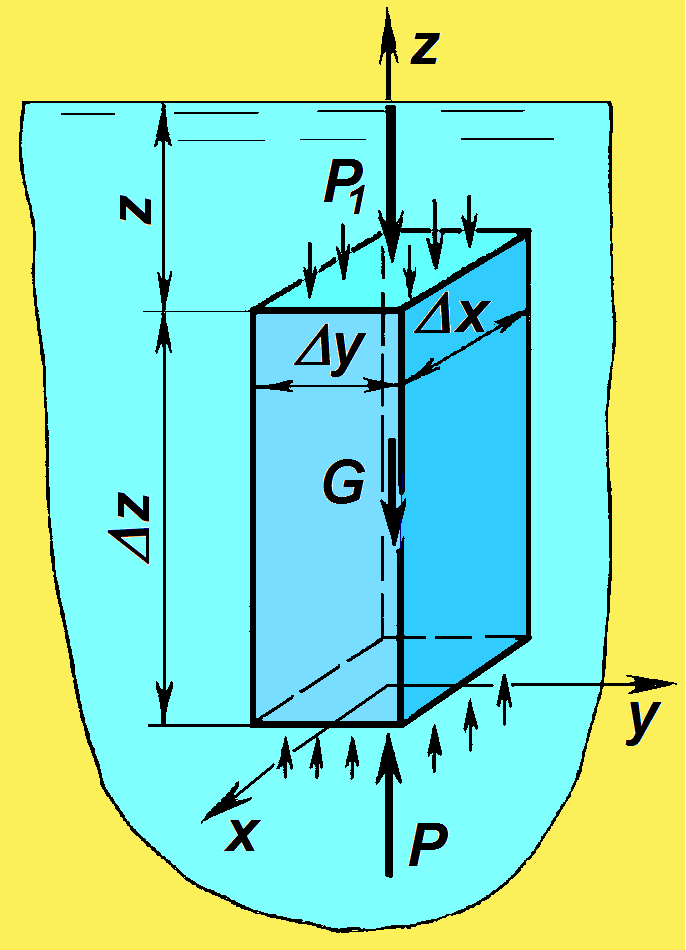 ис 1.

Таким образом истинное давление в точке А будет равно предельному

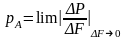
Рис 2.

Выделим в жид-ти, находящейся в покое, объем, имеющий форму призмы со сторонами ∆х, ∆у и ∆z. Рис 2. Рассмотрим равновесие этого объема под действием приложенных к нему сил. Спроектируем силы на вертикальную ось. Очевидно, равнодействующая всех сил, направленных вертикально, будет равна нулю, так как тело находится в равновесии. След. 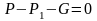или

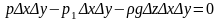
отсюда основное уравнение гидростатики.

Гидростатическое давление в жидкости пропорционально высоте ее слоя и на одинаковой глубине имеет одну и ту же величину во всех точках жидкости.

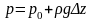_{Если верхнее основание выделенного объема совпадает с поверхностью жидкости, давление на которой равно} то . Поскольку разность Р и Р₁ является подъемной (выталкивающей) силой, то запишем: