4.3 Схема замещения магнитных цепей.

При замещении магнитных цепей электрической кривой ее участок замещения эквивалентным магнитным сопротивлением, а магнитодвижущая сила изображается как источник потока. Для упрощения расчетов принимают всю длину сердечника за один участок, а поток рассеяния (утечка) считают соссредомагнитным в его середине (используется приведенное сопротивление рассеяния). При таких упрощениях схема ЭММ и его электрическая схема замещения имеют вид, показанный на рисунке 5.5.

Рис 5.5- схема замещения ЭММ типа- 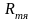-магнитное сопротивление якоря; , -воздушных зазоров (рабочего и нерабочего); , 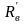-верхних частей якоря и ярма; 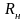, 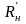-нижней части якоря и ярма;

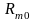-основание; 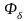-рабочий поток; Ф -конечный поток; 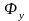-поток утечки; 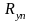-приведенное сопротивление утечки.

Если магнитопровод ненасыщен то,

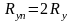
где -полное сопротивление утечки (рассеяния).

Если магнитопровод насыщен (для стопы В=1.1…1,2Тл), то

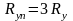
Для расчетов вводится конечный коэффициент рассеяния- отношение максимального потока Ф к потоку в рабочем воздушном зазоре :

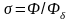(5.10)

Т.к. 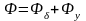, то 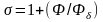(5.11)

4.4 Сила притяжения якоря и магнитная проводимость воздушного зазора.

Точные выражения для силы 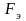и момента 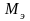, действующих на якорь магнита имеют вид:

;

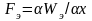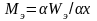
Где 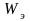полная электромагнитная энергия; х и 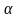- линейное и угловое перемещение якоря.

Для упрощения расчетов учитывают лишь энергию, сосредоточенную в рабочих воздушных зазорах. С учетом этого, например, для ЭММ сплошного тела, у которого сердечника более чем в 2 раза превышает длину основания и для ЭММ с движущимся якорем имеем :

, (5.12)

где - падение магнитной силы обмотки на рабочем воздушном зазоре (ФδRδ); 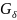– магнитная проводимость рабочего воздушного зазора

1/Rδ).

ЭММ, у которых при изменении δ проводимость рассеивания Gy переменна (ЭММ сплошного типа, у которых длина основания больше длины сердечника или ЭММ типа) имеем:

, (5.13)

Выражение (5.13) для ЭММ сложного типа имеет вид :

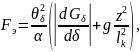(5.14)

где z – длина части сердечника , находящегося в катушке; lk – длина всей катушки; g – удельная проводимость потоков рассеивания:

g = Gy/l

где l – радиус длины поверхности рассеивания

Выражение для Fэ токов ЭММ приводится в литературе

Формула для Mэ отличается от 5.12 – 5.14 только заменой:

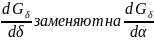
Если принять распределение Фδ в рабочем воздушном зазоре равномерным и пренебречь потоками , то можно воспользоваться формулой Максвелла:

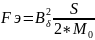, (5.15)

где S – полуось полюса.

Этой формулой пользуются при d/δ >5 (для цилиндрического сечения зазор диаметром d); при a/δ >5 и b/δ > 5 (для прямоугольного сечения зазора длиной a и шириной b). При этом погрешность расчета менее 20%. Так же данной формулой пользуются для определения Fэ при полностью притянутом якоре (при этом ).

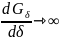Для расчета магнитных цепей необходимо знать магнитные сопротивления (проводимости) и их производных воздушных зазоров различных форм.

При малых воздушных зазорах, когда отношения характерного размера сечения (a, b, d или t) к δ больше 5 согласно (5.5) имеем:

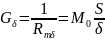; (5.16)

где S – площадь полюсов.

Если условия полости зазора не выполняются, то используется метод, согласно которому пространство воздушного зазора разбивается на элементарные объемы так, чтобы магнитные потоки, пронизывающие эти объемы , были параллельны друг другу. Зная проводимости этих элементарных объемов, общую проводимость воздушного зазора объединяют их суммированием. Выражения для проводимости элементарных воздушных объемов приводятся в специализированной литературе(Элементы приборных устройств: Курсовое проектирование. Учебное пособие для вузов. В 2-x ч Ч.1 Расчеты/ Под ред. О.Ф.Тименко. – М.:Высш.школа, 1978. – 328 с на стр. 280 – 282).