11. Основные термодинамические процессы

• Изохорный – при постоянном объеме;

• Изобарный – при постоянном давлении;

• Изотермический – при постоянной температуре;

• Адиабатный – при отсутствии теплообмена между рабочим телом и окружающей средой.

ИЗОХОРНЫЙ: V=const

• Все тепло, подводимое к системе идет на изменение внутренней энергии системы.

• Уравнение процесса: p₁/T₁=p₂/T₂

• Работа: Lv = 0

• Теплота: Qv = ∆Uv =Mcv(T2 – T1)

ИЗОБАРНЫЙ ПРОЦЕСС p=const

• Теплота, сообщаемая системе, увеличивает её энтальпию.

• Уравнение процесса: v₁/T₁=v₂/T₂

• Работа: Lp = p(V₂ – V₁)

• Теплота: Qp =M_cp(T2 – T1)

• Изменение внутренней энергии: ∆Up = Qp - Lp

ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС Т=const:

• Теплота, сообщаемая системе, тратится на совершение внешней работы.

• Уравнение процесса: p₁v₁=p₂v₂

• Теплота: Qp = LT = RT ln(V2/V1)

• Изменение внутренней энергии: ∆U_T = 0

АДИАБАТНЫЙ ПРОЦЕСС Δq=const:

• Внешняя работа совершается рабочим телом за счет изменения его внутренней энергии.

• Уравнение процесса:

• Работа: L_S = - ∆U_S

• Теплота: Q_S = 0

ПОЛИТРОПНЫЙ ПРОЦЕСС

Политропный процесс, политропический процесс — термодинамический процесс, во время которого удельная теплоёмкость газа остаётся неизменной.

В соответствии с сущностью понятия теплоёмкости , предельными частными явлениями политропного процесса являются изотермически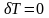й процесс ( ) и адиабатный процесс ( ).

Кривая на термодинамических диаграммах, изображающая политропный процесс, называется «политропа». Для идеального газа уравнение политропы может быть записано в виде:

где р — давление, V — объем газа, n — «показатель политропы».

. Здесь с — теплоёмкость газа в данном процессе, с_р и c_v — теплоемкости того же газа, соответственно, при постоянном давлении и объеме.

В зависимости от вида процесса, можно определить значение n:

• Изотермический процесс: n=1, так как T=const, значит, по закону Бойля — Мариотта 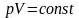, и уравнение политропы вынуждено выглядеть так: .

• Изобарный процесс: n=0, так как , и уравнение политропы вынуждено выглядеть так: .

• Адиабатный процесс: (здесь — показатель адиабаты), это следует из уравнения Пуассона ( ).

• Изохорный процесс: , так как V=const, и в процессе , а из уравнения политропы следует, что , то есть, что , то есть , а это возможно, только если n является бесконечным.

12. Уравнение состояния идеального газа

Уравнение состояния идеального газа (иногда уравнение Клапейрона или уравнение Менделеева — Клапейрона) — формула, устанавливающая зависимость между давлением, молярным объёмом и абсолютной температурой идеального газа. Уравнение имеет вид:

где

• p — давление,

• V_M — молярный объём,

• R — универсальная газовая постоянная

• T — абсолютная температура,К.

Так как , где  — количество вещества, а , где m — масса, M — молярная масса, уравнение состояния можно записать:

Эта форма записи носит имя уравнения (закона) Менделеева — Клапейрона.

В случае постоянной массы газа уравнение можно записать в виде:

Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака:

T=const => pV=const — закон Бойля — Мариотта.

p=const => V/T=const — Закон Гей-Люссака.

V=const => p/T=const — закон Шарля (второй закон Гей-Люссака, 1808 г.)

А в форме пропорции этот закон удобен для расчёта перевода газа из одного состояния в другое.