
Задания для контрольной работы
Номер выполняемого варианта соответствует номеру зачетной книжки студента. Например, студент с номером зачетной книжки 45/10 выполняет вариант 5.
1–10. Решить данную систему уравнений пользуясь формулами Крамера. Сделать проверку полученного решения.
1.
 2.
2.

3.
 4.
4.
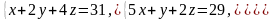
5.
 6.
6.

7.
 8.
8.

9.
 10.
10.

11–20. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
11.
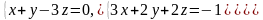 12.
12.

13.
 14.
14.

15.
 16.
16.
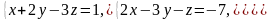
17.
 18.
18.

19.
 20.
20.

21–30. Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
21.
 22.
22.

23.
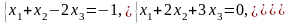 24.
24.
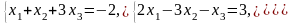
25.
 26.
26.

27.
 28.
28.

29.
 30.
30.

31-40. Туристской фирме требуется не более а трехтонных автобусов и не более в пятитонных автобусов. Отпускная цена автобусов первой марки 20000 у.е., второй марки 40000 у.е. Туристская фирма может выделить для приобретения автобусов не более с у.е. Сколько следует приобрести автобусов каждой марки в отдельности, чтобы их общая (суммарная) грузоподъёмность была максимальной. Решить задачу графическим методом.
31. а = 11 в = 9 с = 460000
32. а = 12 в = 10 с = 520000
33. а = 13 в = 11 с = 580000
34. а = 14 в = 12 с = 640000
35. а = 15 в = 13 с = 700000
36. а = 16 в = 14 с = 760000
37. а = 17 в = 15 с = 820000
38. а = 18 в = 16 с = 880000
39. а = 19 в = 17 с = 940000
40. а = 20 в = 18 с = 1000000
41-50. Исследовать функцию y = f(x) и построить ее график. Найти наибольшее и наименьшее значения функции y = f(x) на отрезке [a, b].
41.
 a
=
1 , b
= 3
a
=
1 , b
= 3
42.
 a
=
1 , b
= 2
a
=
1 , b
= 2
43.
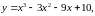 a
= 2 , b
= 3
a
= 2 , b
= 3
44.
 a
=
1 , b
= 2
a
=
1 , b
= 2
45.
 a
= 0 , b
= 4
a
= 0 , b
= 4
46.
 a=
2 , b=
3
a=
2 , b=
3
47.
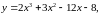 a
=
3 , b
= 0
a
=
3 , b
= 0
48.
 a
= 3
, b
= 1
a
= 3
, b
= 1
49.
 a
= 1 , b
= 4
a
= 1 , b
= 4
50.
 a
=
1 , b
= 4
a
=
1 , b
= 4
5160. Найти неопределённые интегралы и результат интегрирования (в одном примере) проверить дифференцированием.
51.
a)
 б)
б)

в)

52.
а)
 б)
б)

в)

53.
а)
 б)
б)

в)

54.
а)
 б)
б)

в)

55.
а)
 б)
б)

в)

56.
а)
 б)
б)

в)

57.
а)
 б)
б)

в)

58.
а)
 б)
б)

в)
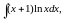
59.
а)
 ,
б)
,
б)

в)
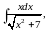
60.
а)
 б)
б)
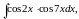
в)

6170. Найти с помощью определенного интеграла площадь плоской фигуры, расположенной в первой четверти и ограниченной заданными параболой, прямой и осью Ох.
61.


62.

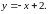
63.


64.


65.


66.


67.


68.

69.

70.
71-80. Задачи по теории вероятностей.
В читальном зале имеется 6 учебников по теории вероятностей, из них 3 в мягком переплёте. Библиотекарь взял 2 учебника. Найти вероятность того, что оба учебника окажутся в мягком переплёте.
Студент знает ответы на 20 вопросов из 25 программных вопросов. Найти вероятность того, что он знает ответы на предложенные ему экзаменатором 3 вопроса.
Для некоторой местности в июле шесть пасмурных дней. Найти вероятность, что первого и второго июля будет ясная погода.
Из 200 рабочих не выполняют норму выработки 15 человек. Найти вероятность того, что два случайно выбранных рабочих не выполняют норму.
Три стрелка стреляют по мишени. Вероятность попадания в цель первым стрелком равна 0.6, вторым – 0.7, третьим – 0.8. Найти вероятность того, что при одном выстреле попадут в цель: а) все три стрелка; б) попадёт хотя бы один из них.
В ящике лежат 20 электрических ламп, из которых 2 нестандартные. Найти вероятность того, что взятые одна за другой две лампочки окажутся стандартными.
Одновременно бросаются две игральные кости. Найти вероятность того, что на каждой кости появится нечётное число очков.
В урне находится 15 шаров, 5 из них красные, а остальные белые. Наугад друг за другом извлекают три шара. Найти вероятность того, что все они окажутся красными.
В бассейне находятся 25 карпов и 5 лещей. Наудачу вылавливают 3 рыбы. Найти вероятность того, что среди них будет хотя бы один лещ.
В офис турфирмы пришли 3 клиента. Вероятность приобрести тур у каждого клиента равна 0.4. Найти вероятность того, что: 1) все клиенты приобретут туры; 2) ни один из них тур не приобретёт.
81 – 90. Задана дискретная случайная величина Х :
-
Х
k
k + 1
k + 2
K + 3
P
0.2
0.3
0.4
0.1
( k – номер варианта студента)
Найти: а) математическое ожидание М(х); б) дисперсию D (x); в) среднее квадратическое отклонение б(х).
Примечание: контрольную работу выполнять в тетради в клетку; писать яркими синими чернилами, четким почерком; условия задач переписывать; на титульном листе необходимо указать (можно в напечатанном виде) следующее: МГИИТ, контрольная работа по математике студента ФИО заочного обучения (4,5 года), курс, группа, шифр (по зачётной книжке), номер варианта. Проверил: ФИО преподавателя.
Примеры решения и оформления заданий (1-70) приведены в учебно-методических пособиях [6] , [7].
Методические указания и примеры решения заданий (71-90)
