6. Законы ньютона

В качестве первого закона Ньютон (1643–1727) принял закон инерции, открытый еще Г. Галилеем

(1564–1642): тело (материальная точка), не подверженное внешним воздействиям, либо находится в покое, либо движется прямолинейно и равномерно. Такое тело называется свободным, а его движение – свободным или движением по инерции. Первый закон Ньютона – Галилея фактически постулирует, что существует система отсчета, в которой все свободные тела движутся прямолинейно и равномерно. Такая система называется инерциальной системой отсчета. Под системой отсчета понимается совокупность тела отсчета, системы координат и часов.

Второй закон Ньютона: ускорение движущегося тела прямо пропорционально действующей на него силе, обратно пропорционально массе тела и направлено по прямой, по которой эта сила действует, т. е.

где a – ускорение тела; F – сила; m – масса тела.

Сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного и прямолинейного движения. Масса тела выступает как коэффициент пропорциональности между силой, действующей на тело, и ускорением (F = ma) и характеризует инертность тела, т. е. степень неподатливости изменению состояния движения.

Третий закон Ньютона: силы взаимодействия двух материальных точек равны по величине, противоположно направлены и действуют вдоль прямой, соединяющей эти материальные точки, т. е.

где F12 – сила, действующая на первое тело со стороны второго; F21 – сила, действующая на второе тело со стороны первого.

Выдающейся заслугой Ньютона было открытие закона всемирного тяготения: два точечных тела притягивают друг друга с силой, прямо пропорциональной произведению их масс, обратно пропорциональной квадрату расстояния между ними и направленной вдоль соединяющей их прямой, т. е.

где γ = 6,7 10-11 м3/(кг • с2) – гравитационная постоянная; m1 и m2 – массы тел; r – расстояние между телами.

7. Принципы относительности галилея

Во всех инерциальных системах отсчета законы классической механики (законы Ньютона) имеют одинаковую форму; в этом сущность механического принципа относительности – принципа относительности Галилея. Он означает, что уравнения динамики при переходе от одной инерциальной системы отсчета к другой не изменяются, т. е. инвариантны по отношению к преобразованиям координат.

x ′ = x – vt , y ′ = y , z ′ =z , t ′ = t ,

где x , y , z и t ; x ′, y ′, z ′ и t ′– координаты тела и время в неподвижной и подвижной системах отсчета соответственно; v – скорость подвижной системы отсчета.

Эти формулы называются преобразованиями Галилея.

Легко показать, что законы динамики Ньютона инвариантны относительно преобразований Галилея. Это объясняется тем, что силы и массы тел одинаковы во всех инерциальных системах отсчета и ускорения тел, которые определяются двойным дифференцированием координат по времени, также одинаковы

(a = d 2 x/dt 2 = d2x'/dt2 = a').

Инвариантами, т. е. величинами, численное значение которых не изменяется при преобразовании координат по Галилею, являются длины и интервалы времени. Покажем это.

Пусть в подвижной системе координат находится неподвижный стержень, координаты концов которого (x´ 1 , y 1´ , z´ 1 ) и (x´ 2 , y´ 2 , z´ 2 ). Это означает, что длина стержня в подвижной системе

Тогда относительно неподвижной системы отсчета стержень движется поступательно и все его точки имеют скорость v. Длиной движущегося стержня, по определению, называется расстояние между координатами его концов в некоторый момент времени. Таким образом, для измерения длины движущегося стержня необходимо одновременно, т. е. при одинаковых показаниях часов неподвижной системы отсчета, расположенных в соответствующих точках, отметить положение концов стержня. Пусть засечки положения концов движущегося стержня сделаны в неподвижной системе координат в момент времени t и характеризуются координатами (х1, у1, z1) и (х2, у2, z2). Тогда для длины стержня в неподвижной системе отсчета будем иметь

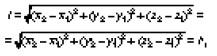
т. е. длина стержня в обеих системах координат одинакова. Это позволяет утверждать, что длина является инвариантом преобразований Галилея.