
- •1)Электромагнитная природа света.Световые волны.Волновое уравнение и простейшие модели световых волн, вытекающие из уравнений максвелла: плоская бегущая волна,сферическая волна.
- •2) Основные характеристики плоских монохроматических волн: фазовая скорость, плотность энергии, интенсивность, поляризация.
- •4) Понятие о временной и пространственной когерентности световых волн.
- •5)Интерференция света: условия и способы наблюдения (опыт юнга, интерферометр майкельсона, интерференция при отражении от тонких пленок).
- •6) Дифракция света: принцип гюйгенса-френеля, дифракция френеля, дифракция фраунгофера.
- •7) Дифракционная решетка.Понятие о голографии.
- •[Править]Формулы
- •7А)явление обращения волного фронта. Понятие об адаптивной оптике.
- •[Править]Методы обращения волнового фронта
- •Вопрос 8. Явление дисперсии и поглощения волн. Понятие о молекулярном рассеянии света.
- •Вопрос 10. Поляризация света.
- •Вопрос 11. Тепловое излучение в замкнутой полости. Закон Кирхгофа. Закон Стефана Больцмана и Вина. Формула Планка.
- •Вопрос 12. Понятие фотона. Фотоэффект и эффект Комптона. Давление света.
- •13)Физические предпосылки возникновения квантовой механики(проблемы не разрешимые классической физикой).Постулаты бора.
- •14)Волны де-бройля.Соотношение неопределенностей гейзенберга. Во́лны де Бро́йля — волны, связанные с любыми микрочастицами и отражающие их волновую природу. Физический смысл
- •Вопрос 15. Постулаты квантовой механики.
- •Получение уравнения Шрёдингера предельным переходом [источник не указан 56 дней]
- •Вопрос 17. Операторы важнейших физических величин: оператор импульса, проекции момента импульса, оператор квадрата момента импульса. Законы сохранения в квантовой физики.
- •Вопрос 18. Квантование момента импульса. Опыт Штерна-Герлаха. Спин.
- •Вопрос 19. Квантомеханическое движение частицы в бесконечно глубокой прямоугольной потенциальной яме.
- •Вопрос 20. Прохождение частиц через потенциальный барьер ( туннельный эффект).
- •Вопрос 21. Квантовый гармонический осциллятор.
- •Вопрос 22. Квантомеханическое описание атома водорода.
- •Вопрос 23. Принцип тождественных частиц. Принцип Паули. Фермионы и бозоны.
Вопрос 18. Квантование момента импульса. Опыт Штерна-Герлаха. Спин.
Как следует из решения уравнения Шредингера для атома водорода, квантовое состояние электрона в этом атоме (можно сказать и квантовое состояние атома) полностью определяется заданием трех квантовых чисел. "Задайте значения квантовых чисел, и я полностью опишу свойства атома" - так может современный физик перефразировать известное изречение Архимеда.
Каждое из квантовых чисел принимает только целочисленные значения и определяет, то есть предсказывает результаты измерения основных физических величин в заданном квантовом состоянии атома.
1. Главное
квантовое число ![]() . Это
квантовое число принимает значения
. Это
квантовое число принимает значения
![]()
и определяет полную энергию электрона в любом квантовом состоянии
|
(5.37) |
Можно
отметить, что эти значения энергии
являются собственными значениями
гамильтониана (5.17a).
Поэтому в связанном состоянии электрон
в атоме водорода имеет дискретный
энергетический спектр, лежащий в области
отрицательных значений и имеющий точку
сгущения ![]() .
.
2. Орбитальное
(азимутальное) квантовое число ![]() . В
квантовых состояниях с заданным значением
главного квантового числа
азимутальное
квантовое число может иметь следующие
значения:
. В
квантовых состояниях с заданным значением
главного квантового числа
азимутальное
квантовое число может иметь следующие
значения:
![]() .
.
Из
выводов предыдущего параграфа следует,
что стационарные волновые функции ![]() ,
описывающие различные квантовые
состояния атома, являются собственными
функциями не только оператора полной
энергии
,
но и оператора квадрата момента
импульса
,
описывающие различные квантовые
состояния атома, являются собственными
функциями не только оператора полной
энергии
,
но и оператора квадрата момента
импульса ![]() ,
причем
,
причем
![]() .
.
Следовательно, в любом квантовом состоянии атом обладает определенным значением квадрата момента импульса, причем модуль орбитального момента импульса движущегося в атоме электрона однозначно определяется орбитальным квантовым числом:
|
(5.38) |
Проанализируем
эту формулу
квантования момента импульса.
Сравнивая ее с условием (5.3) квантования
момента импульса движущегося электрона
в теории Бора, можно заметить, что эти
условия не совпадают. И дело не только
в отличии числовых значений, рассчитанных
по этим формулам. Принципиальное отличие
этих соотношений состоит в том, что в
квантовой механике возможны состояния
атома с нулевым моментом импульса. Во
всех ![]() -состояниях
и, частности, в основном
-состояниях
и, частности, в основном ![]() -состоянии,
когда
-состоянии,
когда ![]() ,
по формуле (5.38)получаем
,
по формуле (5.38)получаем ![]() .
.
Спин электрона. Опыт Штерна и Герлаха.
В 1922 году немецкие физики О. Штерн и В. Герлах поставили опыты, целью которых было измерение магнитных моментов Pm атомов различных химических элементов. Для химических элементов, образующих первую группу таблицы Менделеева и имеющих один валентный электрон, магнитный момент атома равен магнитному моменту валентного электрона, т.е. одного электрона.
Идея опыта заключалась в измерении силы, действующей на атом в сильно неоднородном магнитном поле. Неоднородность магнитного поля должна быть такова, чтобы она сказывалась на расстояниях порядка размера атома. Только при этом можно было получить силу, действующую на каждый атом в отдельности.
Схема опыта изображена на рис. 7.9. В колбе с вакуумом, 10–5 мм рт. ст., нагревался серебряный шарик К, до температуры испарения.
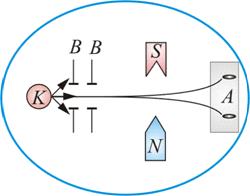
Рис. 7.9 Рис. 7.10
Атомы серебра летели с тепловой скоростью около 100 м/с через щелевые диафрагмы В и, проходя резко неоднородное магнитное поле, попадали на фотопластинку А.
Если бы момент импульса атома (и его магнитный момент ) мог принимать произвольные ориентации в пространстве (т.е. в магнитном поле), то можно было ожидать непрерывного распределения попаданий атомов серебра на фотопластинку с большой плотностью попаданий в середине. Но на опыте были получены совершенно неожиданные результаты: на фотопластинке получились две резкие полосы – все атомы отклонялись в магнитном поле двояким образом, соответствующим лишь двумвозможным ориентациям магнитного момента (рис. 7.10).
Этим доказывался квантовый характер магнитных моментов электронов. Количественный анализ показал, что проекция магнитного момента электрона равна магнетону Бора:
![]()
Таким образом, для атомов серебра Штерн и Герлах получили, что проекция магнитного момента атома (электрона) на направление магнитного поля численно равна магнетону Бора.
Напомним, что
![]()
Опыты Штерна и Герлаха не только подтвердили пространственное квантование моментов импульсов в магнитном поле, но и дали экспериментальное подтверждение тому, что магнитные моменты электронов тоже состоят из некоторого числа «элементарных моментов», т.е. имеют дискретную природу. Единицей измерения магнитных моментов электронов и атомов является магнетон Бора (ħ – единица измерения механического момента импульса).
Кроме того, в этих опытах было обнаружено новое явление. Валентный электрон в основном состоянии атома серебра имеет орбитальное квантовое число l = 0 (s-состояние). Но при l = 0 (проекция момента импульса на направление внешнего поля равна нулю). Возник вопрос, пространственное квантование какогомомента импульса обнаружилось в этих опытах и проекция какого магнитного момента равна магнетону Бора.
В 1925 г. студенты Геттингенского университета Гаудсмит и Уленбек предположили существование собственного механического момента импульса у электрона (спина) и, соответственно, собственного магнитного момента электрона Pms.
Введение понятия спина сразу объяснило ряд затруднений, имевшихся к тому времени в квантовой механике. И в первую очередь – результатов опытов Штерна и Герлаха.
Авторы дали такое толкование спина: электрон – вращающийся волчок. Но тогда следует, что «поверхность» волчка (электрона) должна вращаться с линейной скоростью, равной 300 с, где с – скорость света. От такого толкования спина пришлось отказаться.
В современном представлении – спин, как заряд и масса, есть свойство электрона.
П. Дирак впоследствии показал, что существование спина вытекает из решения релятивистского волнового уравнения Шредингера.
Из общих выводов квантовой механики следует, что спин должен быть квантован:
![]() ,где s – спиновое
квантовое число.
,где s – спиновое
квантовое число.
Численное
значение спина электрона:
![]() .
.

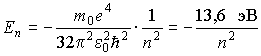 .
.