
- •1) Основные элементарные функции их свойства и графики.
- •2) Определение производной функции в точке. Таблица производных.
- •4) Промежутки возрастания и убывания функции. Максимум и минимум функции.
- •5) Первообразная. Неопределённый интеграл. Таблица интегралов.
- •6) Определение и свойства определённого интеграла.
- •10) Классическое и статистическое определение вероятности событий.
- •11) Теоремы сложения вероятностей.
- •12) Теоремы умножений вероятностей.
- •13) Формула Бернулли.
- •14) Случайные величины дискретные и непрерывные.
- •15) Математическое ожидание и дисперсия дискретной случайной величины.
- •16) Вариационный ряд. Статистическое распределение выборки.
- •17) Полигон частот.
- •18) Гистограмма частот.
1) Основные элементарные функции их свойства и графики.
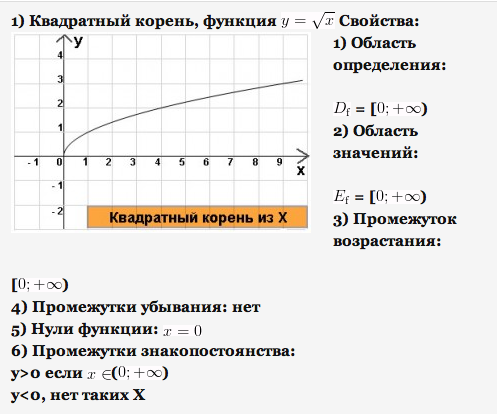

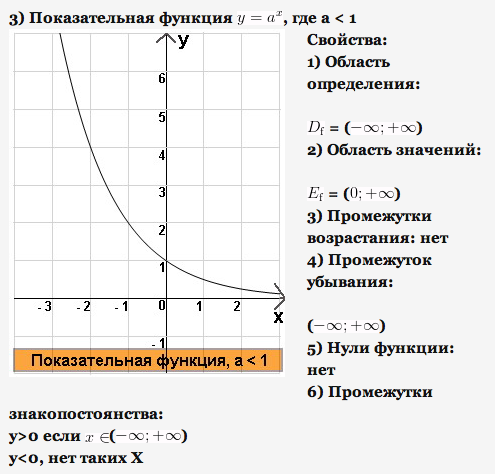
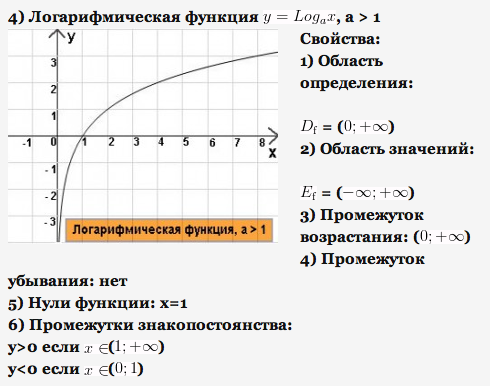
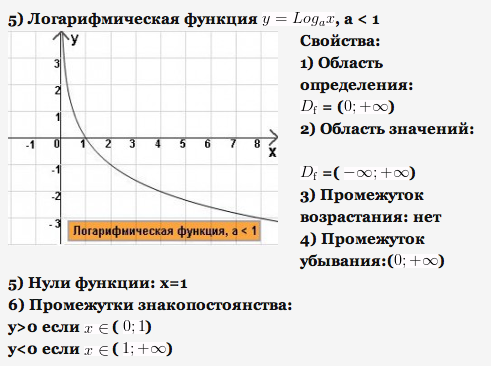


2) Определение производной функции в точке. Таблица производных.
Определение
производной функции в точке.
Пусть
функция f(x)
определена на промежутке (a;
b),
![]() и
и
![]() - точки этого промежутка. Производной
функции f(x)
в точке
называется предел отношения приращения
функции к приращению аргумента при
- точки этого промежутка. Производной
функции f(x)
в точке
называется предел отношения приращения
функции к приращению аргумента при
![]() .
Обозначается
.
Обозначается
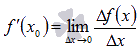 .
Когда
последний предел принимает конкретное
конечное значение, то говорят о
существовании конечной
производной в точке.
Если предел бесконечен, то говорят, что
производная
бесконечна в данной точке.
Если же предел не существует, то и
производная
функции в этой точке не существует.
Функцию
f(x)
называют дифференцируемой
в точке
,
когда она имеет в ней конечную
производную.
Если функция f(x)
дифференцируема в каждой точке некоторого
промежутка (a;
b),
то функцию называют дифференцируемой
на этом промежутке. Таким образом, любой
точке x
из промежутка (a;
b)
можно поставить в соответствие значение
производной функции в этой точке
.
Когда
последний предел принимает конкретное
конечное значение, то говорят о
существовании конечной
производной в точке.
Если предел бесконечен, то говорят, что
производная
бесконечна в данной точке.
Если же предел не существует, то и
производная
функции в этой точке не существует.
Функцию
f(x)
называют дифференцируемой
в точке
,
когда она имеет в ней конечную
производную.
Если функция f(x)
дифференцируема в каждой точке некоторого
промежутка (a;
b),
то функцию называют дифференцируемой
на этом промежутке. Таким образом, любой
точке x
из промежутка (a;
b)
можно поставить в соответствие значение
производной функции в этой точке
![]() ,
то есть, мы имеем возможность определить
новую функцию
,
которую называют производной
функции f(x)
на интервале (a;
b).
Операция
нахождения производной называется
дифференцированием.
Проведем
разграничения в природе понятий
производной функции в точке и на
промежутке: производная функции в точке
– это есть число, а производная функции
на промежутке – это есть функция.
,
то есть, мы имеем возможность определить
новую функцию
,
которую называют производной
функции f(x)
на интервале (a;
b).
Операция
нахождения производной называется
дифференцированием.
Проведем
разграничения в природе понятий
производной функции в точке и на
промежутке: производная функции в точке
– это есть число, а производная функции
на промежутке – это есть функция.
ТАБЛИЦА ПРОИЗВОДНЫХ:

3) Производная сложной функции.
Сложная
функция
– это функция, аргументом которой также
является функция.
С нашей точки
зрения, это определение наиболее понятно.
Условно можно обозначать как f(g(x)).
То есть, g(x)
как бы аргумент функции f(g(x)).
К
примеру, пусть f
– функция арктангенса, а g(x)
= lnx
есть функция натурального логарифма,
тогда сложная функция f(g(x))
представляет собой arctg(lnx).
Еще пример: f
– функция возведения в четвертую
степень, а
![]() - целая рациональная функция (смотрите
классификацию
элементарных функций),
тогда
- целая рациональная функция (смотрите
классификацию
элементарных функций),
тогда
![]() .
В
свою очередь, g(x)
также может быть сложной функцией.
Например,
.
В
свою очередь, g(x)
также может быть сложной функцией.
Например,
 .
Условно такое выражение можно обозначить
как
.
Условно такое выражение можно обозначить
как
![]() .
Здесь f
– функция синуса,
.
Здесь f
– функция синуса,
![]() - функция извлечения квадратного корня,
- функция извлечения квадратного корня,
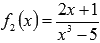 - дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом
- дробная рациональная функция. Логично
предположить, что степень вложенности
функций может быть любым конечным
натуральным числом
![]() .
Часто
можно слышать, что сложную функцию
называют композицией
функций.
Формула
нахождения производной сложной
функции.
.
Часто
можно слышать, что сложную функцию
называют композицией
функций.
Формула
нахождения производной сложной
функции.
![]()
4) Промежутки возрастания и убывания функции. Максимум и минимум функции.
Определение возрастающей функции.
Функция
y
= f(x)
возрастает на интервале X,
если для любых
![]() и
и
![]() выполняется неравенство
выполняется неравенство
![]() .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
.
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение убывающей функции.
Функция
y
= f(x)
убывает на интервале X,
если для любых
и
![]() выполняется неравенство
выполняется неравенство
![]() .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a; b), то есть при x = a и x = b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.
К
примеру, из свойств основных элементарных
функций мы знаем, что y
= sinx
определена и непрерывна для всех
действительных значений аргумента.
Поэтому, из возрастания функции синуса
на интервале
 мы можем утверждать о возрастании на
отрезке
мы можем утверждать о возрастании на
отрезке
 .
.
Точку
![]() называют точкой
максимума
функции y
= f(x),
если для всех x из ее окрестности
справедливо неравенство
называют точкой
максимума
функции y
= f(x),
если для всех x из ее окрестности
справедливо неравенство
![]() .
Значение функции в точке максимума
называют максимумом
функции
и обозначают
.
Значение функции в точке максимума
называют максимумом
функции
и обозначают
![]() .
.
Точку
называют точкой
минимума
функции y
= f(x),
если для всех x из ее окрестности
справедливо неравенство
![]() .
Значение функции в точке минимума
называют минимумом
функции
и обозначают
.
Значение функции в точке минимума
называют минимумом
функции
и обозначают
![]() .
.
Под
окрестностью точки
понимают интервал
![]() ,
где
,
где
![]() - достаточно малое положительное число.
- достаточно малое положительное число.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Достаточные признаки возрастания и убывания функции.
На основании достточных признаков находятся промежутки возрастания и убывания функции.
если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:
найти область определения функции;
найти производную функции
решить неравенства f’(x)>0 и f’(x)<0 на области определения;
к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.
Достаточные признаки экстремума функции.
Пусть функция y = f(x) дифференцируема в -окрестности точки , а в самой точке непрерывна. Тогда
если
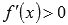 при
при
 и
и
 при
при
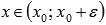 ,
то
- точка максимума;
,
то
- точка максимума;
если при и при , то - точка минимума.
Другими словами:
если в точке функция непрерывна и в ней производная меняет знак с плюса на минус, то - точка максимума;
если в точке функция непрерывна и в ней производная меняет знак с минуса на плюс, то - точка минимума.
