Вопрос 45. Методом трапеций

uses crt;

var a,b: byte; s: real;

begin

clrscr;

write('введите значения параметров a и b: ');

readln(a,b);

s:=(2*b*sqrt(b))/3-(2*a*sqrt(a))/3;

write('площадь криволинейной трапеции = ',s:4:2);

end.

Сначала выведем формулу трапеций. Далее запишем оценку абсолютной погрешности метода и подробно разберем решение характерных примеров. В заключении сравним метод трапеций с методом прямоугольников.

Поставим задачу.

Пусть нам требуется вычислить определенный интеграл 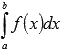, где y = f(x) непрерывна на отрезке [a; b].

Разобьем отрезок [a; b] на n равных интервалов длины h точками . В этом случае шаг разбиения находим как и узлы определяем из равенства .

Рассмотрим функцию на элементарных отрезках .

Возможны четыре случая (на рисунке показаны простейшие из них, к которым все сводится при увеличении n):

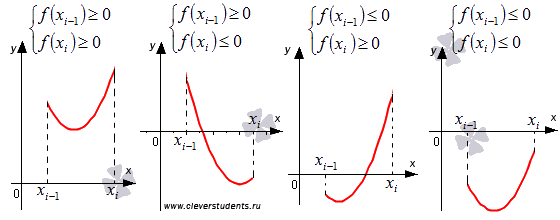
На каждом отрезке заменим функцию y = f(x) отрезком прямой, проходящей через точки и . На рисунке показаны синими линиями:

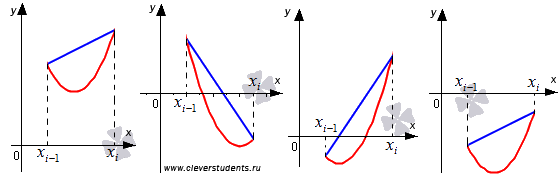
В качестве приближенного значения интеграла 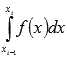возьмем выражение , то есть , .

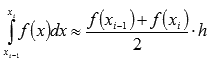Давайте выясним, что означает в геометрическом смысле записанное приближенное равенство. Мы знаем, что площадь трапеции находится как произведение полу суммы оснований на высоту. Следовательно, в первом случае площадь криволинейной трапеции приближенно равна площади трапеции с основаниями и высотой h, в последнем случае определенный интеграл приближенно равен площади трапеции с основаниями и высотой h, взятой со знаком минус. Во втором и третьем случаях приближенное значение определенного интеграла равно разности площадей красной и синей областей, изображенных на рисунке ниже.

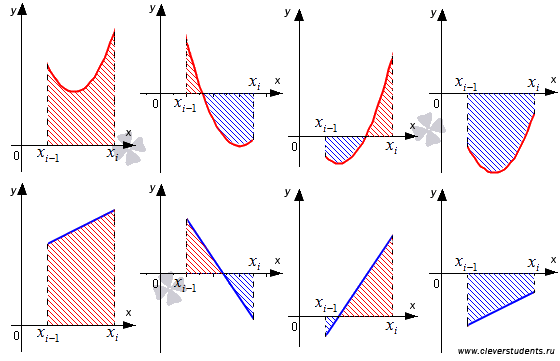
Теперь стало понятно, почему рассматриваемый метод численного интегрирования называется методом трапеций.

В силу пятого свойства определенного интеграла .

Если вместо интегралов подставить их приближенные значения, то получим формулу метода трапеций:

Абсолютная погрешность метода трапеций оценивается как

.

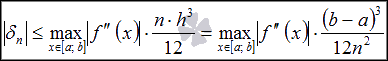
Графическая иллюстрация метода трапеций.

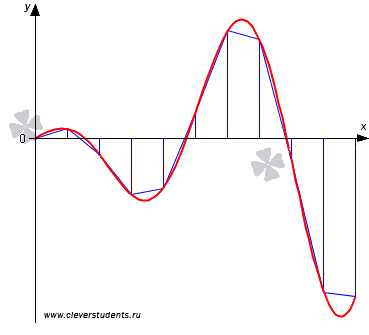
Разберем метод трапеций на примере.

В основном встречаются две разновидности заданий:

либо вычислить определенный интеграл методом трапеций для данного числа разбиения отрезка n,

либо найти приближенное значение определенного интеграла с требуемой точностью.

Следует заметить, что при заданном n промежуточные вычисления следует проводить с достаточной степенью точности, скажем, до четырех-пяти знаков после запятой.

Если требуется вычислить определенный интеграл с заданной точностью, к примеру, до 0.01, то промежуточные вычисления рекомендуем проводить на два-три порядка точнее, то есть, до 0.0001 - 0.00001.

Для примера возьмем определенный интеграл, значение которого мы можем вычислить по формуле Ньютона-Лейбница, чтобы можно было сравнивать этот результат с приближенным значением, полученным по методу трапеций.

Итак, .

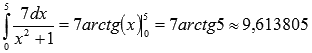Пример.

Вычислить определенный интеграл 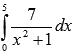методом трапеций для n = 10.

Решение.

Формула метода трапеций имеет вид 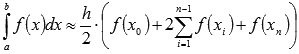. То есть, для ее применения нам достаточно вычислить шаг h по формуле , определить узлы и вычислить соответствующие значения подынтегральной функции .

Вычислим шаг разбиения: .

Определяем узлы и вычисляем значения подынтегральной функции в них (будем брать четыре знака после запятой):

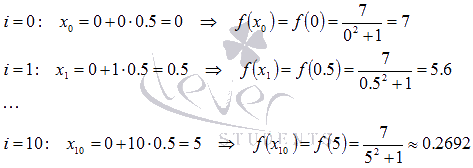
Результаты вычислений для удобства представляем в виде таблицы:

Подставляем их в формулу метода трапеций:

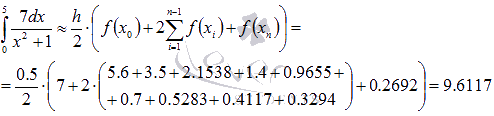
Полученное значение совпадает до сотых со значением, вычисленным по формуле Ньютона-Лейбница.