7. Вычисление кратных интегралов

7.1. Вычисление двойного интеграла в декартовых координатах

Рассмотрим ограниченную область .

Будем называть D правильной в направлении оси Oy, если она ограничена линиями и каждая прямая, параллельная оси Oy, проходящая через внутреннюю точку области, пересекает границу области D ровно в двух точках (рис. 7.1).

Н ижнюю из них (1) будем называть точкой входа, верхнюю (2) – точкой выхода.

Аналогично определяется область, правильная в направлении оси Ox (рис. 7.2).

О бласть, правильная в направлении обеих осей, называется правильной (нормальной).

О бласти более сложной формы обычно без особых затруднений можно разбить на несколько правильных областей. В качестве упражнения проделайте это с областью, изображенной на рис. 7.3 (область имеет «дыру»).

При вычислении двойного интеграла

(7.1)

б удем считать, что область D правильная, а

Разобьем область D на элементарные прямоугольные участки прямыми, параллельными осям координат (рис. 7.4). Очевидно, что – площадь участка . На основании этого элемент площади в декартовых координатах записывают в виде Внутри каждого прямоугольника выберем точку .

Выведем формулу для вычисления двойного интеграла (7.1)

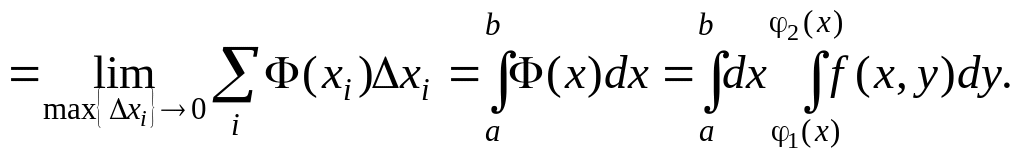
Итак,

(7.2)

Интеграл, стоящий в правой части равенства (7.2), называется двукратным (или повторным) интегралом.

Из полученной формулы следует правило вычисления двойного интеграла: для вычисления интеграла (7.1) нужно проинтегрировать функцию f(x, y) по y (считая х постоянным) от до , затем проинтегрировать полученный результат по х в пределах от а до b (см. схему на рис. 7.5).

Рис. 7.5 Рис. 7.6

Аналогично можно вычислить интеграл (7.1), выполняя сначала интегрирование в направлении оси Ox, а затем – в направлении оси Oy:

(7.3)

(см. схему на рис. 7.6).

В двукратном интеграле (7.2) интеграл

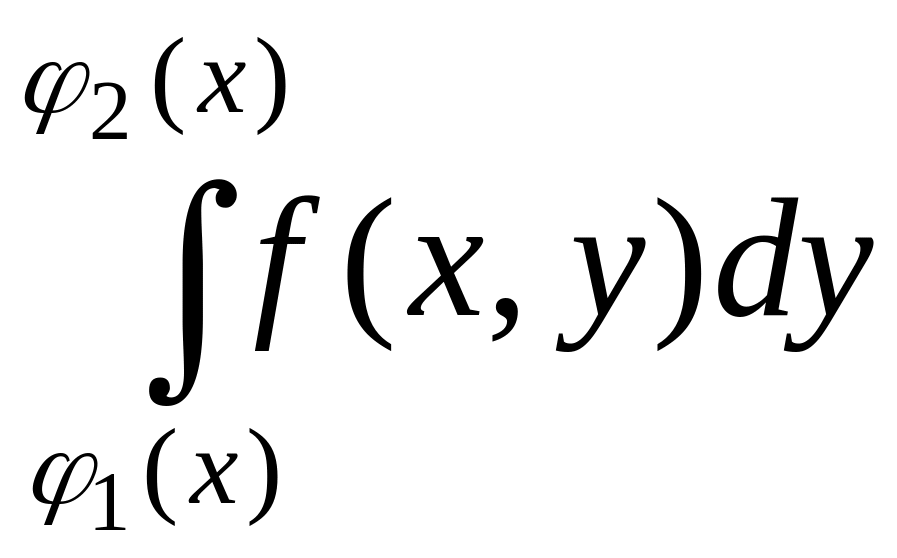
называется внутренним, а

– внешним (в (7.3) – аналогично).

7.2. Вычисление тройного интеграла в декартовых координатах

Область будем называть правильной в направлении оси Oz, если:

1. любая прямая, параллельная оси Oz и проходящая через внутреннюю точку области V, пересекает ее границу ровно в двух точках;

2. п роекцией области V на плоскость Oxy является правильная область S (рис. 7.12).

Аналогично определяется область, правильная в направлении осей Ox и Oy.

При вычислении тройного интеграла

будем считать, что область V правильная в направлении оси Oz, а . «Снизу» область V ограничивает поверхность , а «сверху» – . Проекцию S области V на плоскость Oxy в направлении оси Oy ограничивают кривые и

(рис. 7.13).

В декартовых прямоугольных координатах элемент объёма записывается в виде

Получим формулу для вычисления тройного интеграла в декартовых координатах:

= .

Рис. 7.13

Итак,

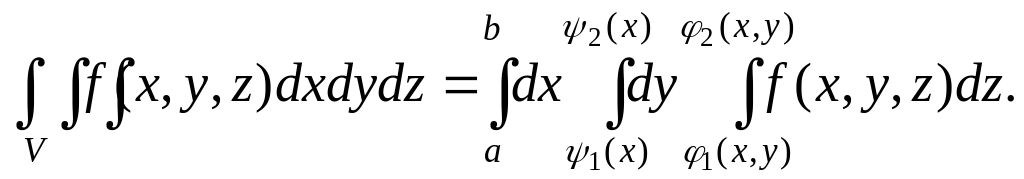(7.4)

Интеграл, стоящий в правой части формулы (7.4), называется трехкратным интегралом.

Интегрирование по области V, правильной в направлении оси Ox или Oy, выполняется аналогично.

Сформулируйте самостоятельно правило вычисления тройного интеграла.