
- •Ответы на вопросы по Математическому Анализу (II семестр)
- •4) Определенный интеграл Риммана.
- •10) Несобственный интеграл II-ого рода (от разрывной функции)
- •11) Теоремы сравнения.
- •12) Несобственный интеграл( общий случай)
- •13) Примеры применения определенных интегралов.
- •14) Интегралы от четных и нечетных функций, на симметричных приделах интегрирования
- •15) Гамма-функция, бета-функция:
- •16) Сходимость числового ряда.
- •17) Признак сравнения рядов.
- •18) Абсолютная сходимость
- •19) Радикальный признак сходимости Коши
- •20) Признак сходимости Деламбера.
- •21) Признак Лейбница
- •22) Интегральный признак сходимости (Коши).
- •23) Степенные ряды, теорема Абеля:
- •27) Вещественное значение ряда Фурье
- •29) Разложение четных и нечетных функций:
Ответы на вопросы по Математическому Анализу (II семестр)
1)Непрерывность. Пусть функция y=f(x) определена в точке x0 и в некоторой окрестности этой точки. Функция y=f(x) называется непрерывной в точке x0, если существует придел в этой точке и он равен значению функции в этой точке т.е.
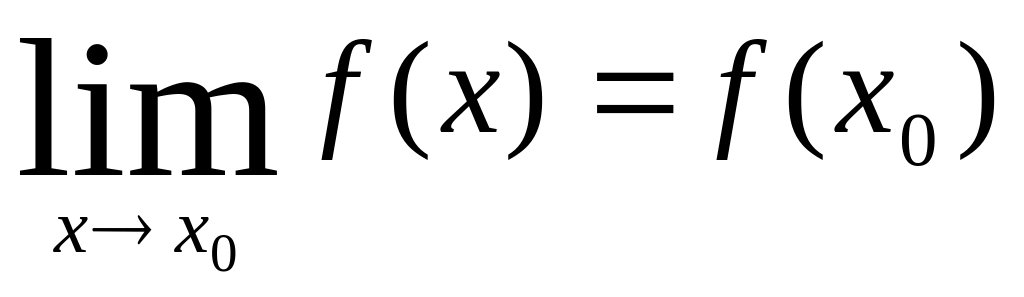
Функция y=f(x) называется непрерывной в интервале (a,b), если она непрерывна в каждой точке этого интервала
Функция y=f(x)
называется непрерывной на отрезке
[a,b],
если она непрерывна в интервале (a,b)
и в точке x=a
непрерывна справа(![]() ),
а в точке x=b
непрерывна слева(
),
а в точке x=b
непрерывна слева(![]() ).
).
2) Производная. Производной функции y=f(x) в точке x0 называется предел отношения приращения функции к приращению аргумента когда приращения аргумента стремится к нулю.
![]()
Геометрический смысл: производная это тангенс угла на клона касательной к кривой.
3) Неопределенный интеграл. Множество всех первообразных функций F(x)+C для f(x) называется неопределенным интегралом от функции f(x)
![]()
f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение, x – переменная интегрирования.
Геометрический смысл: Геометрически неопределенный интеграл представляет собой семейство «параллельных» кривых y=F(x)+C (каждому числовому значению C соответствует определенная кривая семейства). График каждой первообразной (кривой) называют интегральной кривой.
Свойства:
1. дифференциал от непрерывного интеграла равен подынтегральному выражению, а производная неопределенного интеграла равна подынтегральной функции:
![]()
2. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной:
![]()
3. Постоянный множитель можно выносить за знак интеграла
![]()
![]()
4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:
![]()
5. Инвариантность формулы интегрирования.
Если
![]() ,
то и
,
то и
![]() -
произвольная функция, имеющая непрерывную
производную.
-
произвольная функция, имеющая непрерывную
производную.
4) Определенный интеграл Риммана.
Д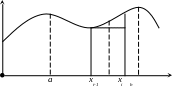 ана
функция f(x)
на отрезке [a,b],
a<b.
ана
функция f(x)
на отрезке [a,b],
a<b.
Разобьем её на элементарные участки.
a=x0<x1<x2<x3<…<xn=b
![]() Є(xi-1,
xi),
Δxi=(xi-xi-1),
составим интегральную сумму
Є(xi-1,
xi),
Δxi=(xi-xi-1),
составим интегральную сумму
![]()
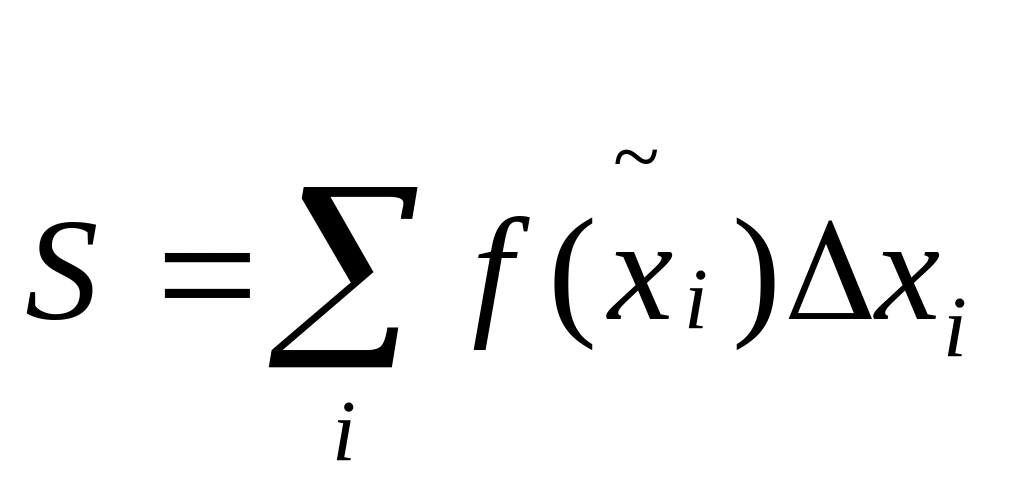
(Максимальная длина промежутка стремиться к нулю).
Если существует конечный придел S независящий, ни от способа разбиения промежутка ни от выбора точек x,такой придел называется определенным интегралом функции f(x) на отрезке [a,b](область интегрирования) т.е.
![]()
Теорема Коши(существование определенного интеграла):
Если функция y= f(x)
непрерывна на отрезке [a,b],
то определенный интеграл
![]() существует.
существует.
Свойства:
1. Определенный интеграл не зависит от обозначения переменной интегрирования:
![]()
2. Определенный интеграл с одинаковыми приделами интегрирования равен нулю.
![]()
3. Для любого действительного числа
с:
![]()
4.![]()
Геометрический смысл: Определенный интеграл от неотрицательной функции числено равен площади криволинейной тропеции.
5) Формула Ньютона-Лейбница
Если функция y=f(x) непрерывна на отрезке [a,b] и F(x) - какая-либо ее первообразная на [a;b](F’(x)=f(x)), то иемеет место формула:
![]()
6) Теорема о среднем.
Если функция f(x) непрерывна на отрезке [a;b], то существует точка с Є[a;b] такая, что
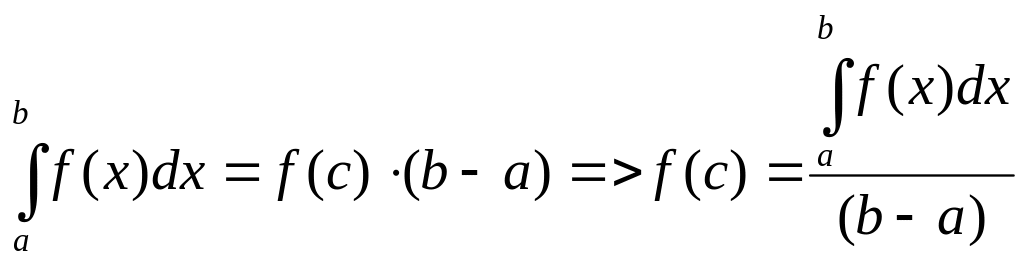
7) Метод интегрирования подстановкой (заменой переменной).
Необходимо найти интеграл:
![]() сделаем подстановку
сделаем подстановку
![]() тогда
тогда
![]()
![]()
Иногда целесообразно подбирать
подстановку в виде
![]() тогда
тогда
![]()
8) Метод интегрирования по частям
Пусть u=u(x) и v=v(x)- функции имеющие непрерывные производные тогда d(uv)=udv+vdu интегрируя это равенство получаем:
![]()
Несобственный интеграл- определенный интегралом непрерывной функции, но с бесконечным промежутком интегрирования(I-ого рода)или определенный интеграл с конечным промежутком интегрирования, но от функции, имеющий на нём бесконечный разрыв.
9) Несобственные интегралы 1-ого рода (с бесконечными промежутком интегрирования)
Пусть функция f(x)
непрерывна на промежутке [a;+∞]
если существует конечный придел
![]() то его называют несобственным интегралом
первого рода и записывают как:
то его называют несобственным интегралом
первого рода и записывают как:![]() .
.
Если = то говорят что интеграл сходится, если же придела не существует либо он бесконечен то интеграл расходится.
Аналогично определяется интеграл
![]() =
=![]()
Несобственный интеграл с двумя бесконечными формулами определяется формулой:
![]() =
=![]() +
+![]()
Признаки сходимости:
1. Признак сравнения. Если на промежутке
[a;+∞] непрерывные
функции f(x)
и g(x)
удовлетворяют условию
![]() ,
nто из сходимости
,
nто из сходимости
![]() следует сходимость
следует сходимость
![]() ,
а из расходимости
следует расходимость
,
а из расходимости
следует расходимость
2. Если существует придел
![]() (f(x)>0
и g(x)>0), то
интегралы
и
сходятся
или расходятся одновременно.
(f(x)>0
и g(x)>0), то
интегралы
и
сходятся
или расходятся одновременно.
