
- •Глава 10. Интегралы, зависящие от параметра. §10.1. Собственные интегралы, зависящие от параметра (изоп).
- •Теорема 1 (о непрерывности изоп). Если функция непрерывна на прямоугольнике , то изоп есть непрерывная функция на .
- •Теорема 2 (об интегрируемости изоп). Если функция непрерывна на , то изоп есть интегрируемая на функция, причём
- •Теорема 3 (о дифференцируемости изоп). Если функция и её частная производная непрерывны на , то изоп есть непрерывно дифференцируемая на функция, причём , (5)
- •Пример 1. Вычислить интеграл .
- •§10.2. Несобственные интегралы, зависящие от параметра (низоп).
- •Пример 1. Исследовать на равномерную сходимость интеграл на отрезках: 1) ; 2) .
- •Теорема 1 (Признак Вейерштрасса равномерной сходимости низоп). Если функция интегрируема по на отрезке и если
- •Теорема 2 (о непрерывности низоп). Если функция непрерывная на , а низоп (1) равномерно сходится на , то функция из (1) непрерывная на .
- •Теорема 3 (об интегрируемости низоп). Если функция непрерывная на , а низоп (1) равномерно сходится на , то низоп есть интегрируемая на функция, причём
- •§10.3. Гамма – и Бэта – функции Эйлера.
- •§10.4. Интеграл Дирихле.
§10.4. Интеграл Дирихле.
Рассмотрим
интеграл
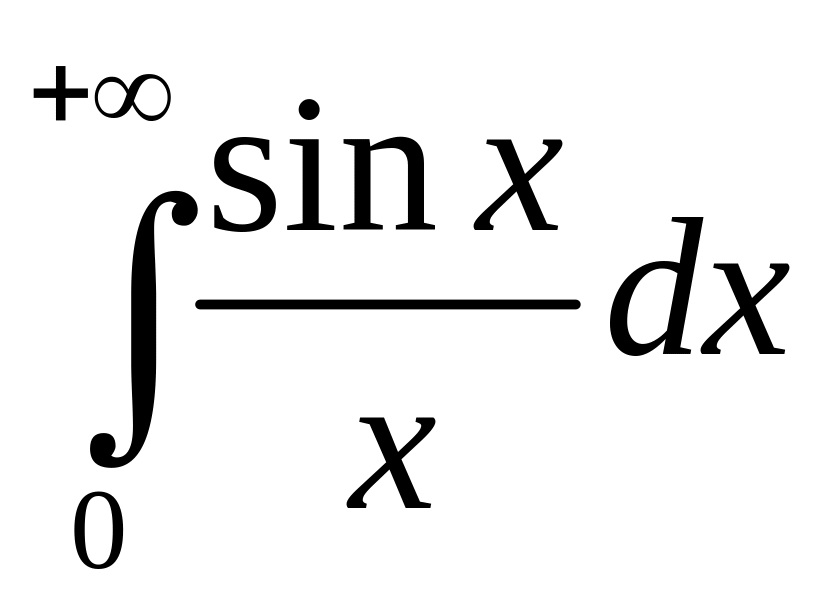 .
Он сходится
по признаку
Дирихле:
первообразная
от
.
Он сходится
по признаку
Дирихле:
первообразная
от
![]() ограничена,
а функция
ограничена,
а функция
![]() монотонно
стремится к
нулю
при
монотонно
стремится к
нулю
при
![]() .
В
точке
.
В
точке
![]() он
существует как
обычный
определённый
интеграл.
он
существует как
обычный
определённый
интеграл.
Для вычисления значения интеграла Дирихле рассмотрим функцию
 (1)
(1)
Покажем,
что функция
![]() непрерывна при
непрерывна при
![]() .
Для этого
сначала
покажем,
что НИЗОП (1)
равномерно сходится при
.
Вычислим
первообразную
.
Для этого
сначала
покажем,
что НИЗОП (1)
равномерно сходится при
.
Вычислим
первообразную

откуда
![]() (2)
(2)
Поскольку
![]() ,
а
,
а
 ,
,
то
![]() .
(3)
.
(3)
Пользуясь методом интегрирования по частям и неравенством (3), получим
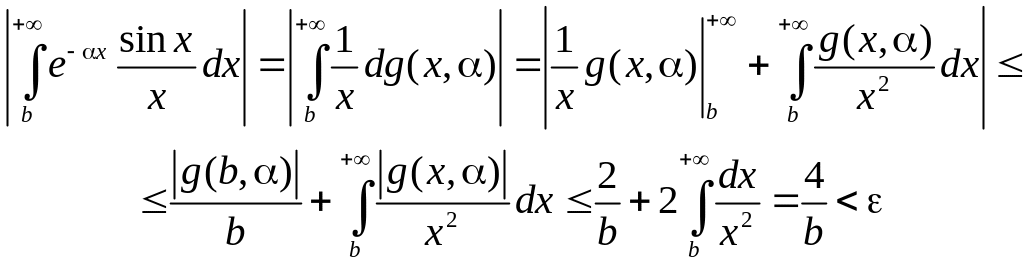
при
![]() и
и
![]() ,
что означает
равномерную
сходимость
НИЗОП (1)
при
.
,
что означает
равномерную
сходимость
НИЗОП (1)
при
.
На основании
теоремы 2 §10.3 функция
непрерывна на
![]() .
.
Для вычисления
производной
![]() рассмотрим
интеграл, получаемый
из интеграла
(1)
после
дифференцирования его
подынтегральной
функции
по параметру
рассмотрим
интеграл, получаемый
из интеграла
(1)
после
дифференцирования его
подынтегральной
функции
по параметру
![]()
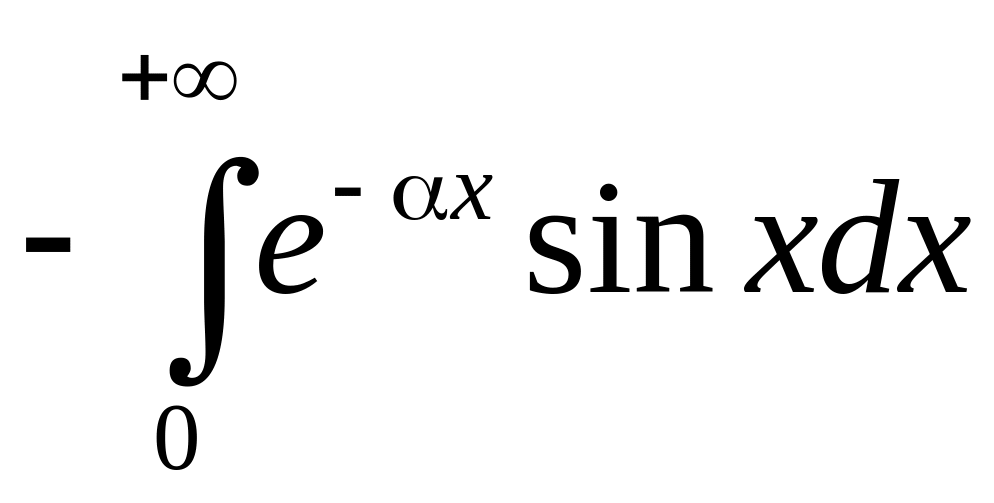 .
(4)
.
(4)
Этот интеграл
равномерно сходится на каждом
отрезке
![]() ,
поскольку
,
поскольку
![]() и
и
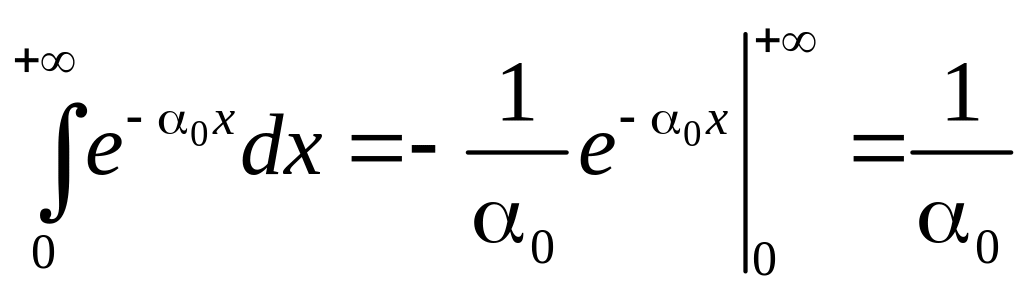 – сходится (признак
Вейерштрасса).
Тогда по
теореме
4 §10.2 при
– сходится (признак
Вейерштрасса).
Тогда по
теореме
4 §10.2 при
![]() имеем
имеем
=
![]()
 =
=![]() .
(5)
.
(5)
Поскольку
![]() и
можно
выбирать
произвольно,
то равенство
(5) имеет место
при
и
можно
выбирать
произвольно,
то равенство
(5) имеет место
при
![]() .
Интегруя
(5) по
,
получим
.
Интегруя
(5) по
,
получим
![]() .
(6)
.
(6)
Поскольку
 (мы показывали
ранее, что
(мы показывали
ранее, что
![]() ),
то
),
то
 .
Поэтому
.
Поэтому
![]() .
Из
равенства
(6) найдём
константу
С:
.
Из
равенства
(6) найдём
константу
С:
![]() .
.
Таким образом, из
(6) получаем
![]() .
(7)
.
(7)
Из
непрерывности
следует
 .
.
Таким образом,
 – интеграл Дирихле.
– интеграл Дирихле.
Из
этой
формулы следует
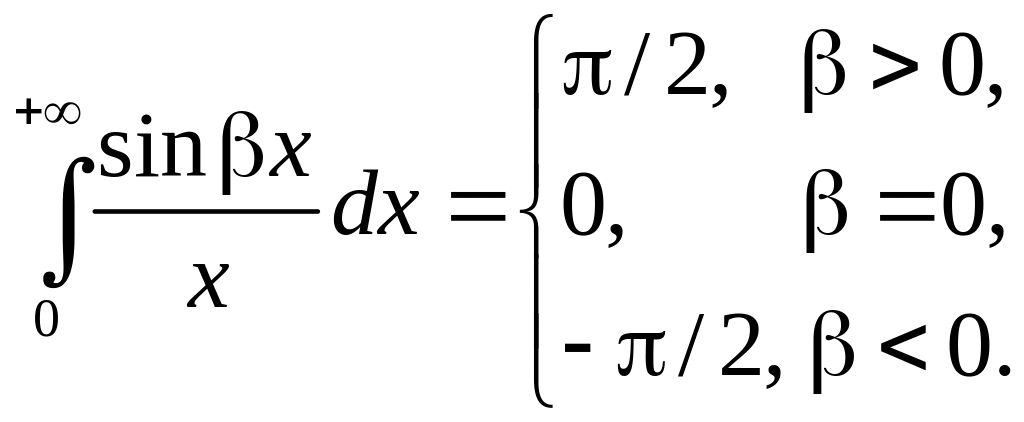
(Достаточно
в интеграле сделать
замену
![]() ,
або
,
або
![]() .)
.)
