
- •Глава 10. Интегралы, зависящие от параметра. §10.1. Собственные интегралы, зависящие от параметра (изоп).
- •Теорема 1 (о непрерывности изоп). Если функция непрерывна на прямоугольнике , то изоп есть непрерывная функция на .
- •Теорема 2 (об интегрируемости изоп). Если функция непрерывна на , то изоп есть интегрируемая на функция, причём
- •Теорема 3 (о дифференцируемости изоп). Если функция и её частная производная непрерывны на , то изоп есть непрерывно дифференцируемая на функция, причём , (5)
- •Пример 1. Вычислить интеграл .
- •§10.2. Несобственные интегралы, зависящие от параметра (низоп).
- •Пример 1. Исследовать на равномерную сходимость интеграл на отрезках: 1) ; 2) .
- •Теорема 1 (Признак Вейерштрасса равномерной сходимости низоп). Если функция интегрируема по на отрезке и если
- •Теорема 2 (о непрерывности низоп). Если функция непрерывная на , а низоп (1) равномерно сходится на , то функция из (1) непрерывная на .
- •Теорема 3 (об интегрируемости низоп). Если функция непрерывная на , а низоп (1) равномерно сходится на , то низоп есть интегрируемая на функция, причём
- •§10.3. Гамма – и Бэта – функции Эйлера.
- •§10.4. Интеграл Дирихле.
Глава 10. Интегралы, зависящие от параметра. §10.1. Собственные интегралы, зависящие от параметра (изоп).
Пусть
на прямоугольнике
![]() определена функция
определена функция
![]() .
Если
.
Если
![]() функция
интегрируема по
функция
интегрируема по
![]() на
на
![]() ,
то интеграл
,
то интеграл
 есть
функция от
параметра
есть
функция от
параметра
![]() ,
определённая
на
,
определённая
на
![]() .
При этом
.
При этом
 (1)
(1)
называют интегралом, зависящим от параметра y (ИЗОП).
Если функция
![]() определена на множестве более
общего
вида
определена на множестве более
общего
вида
![]()
и на
![]() существует интеграл
существует интеграл
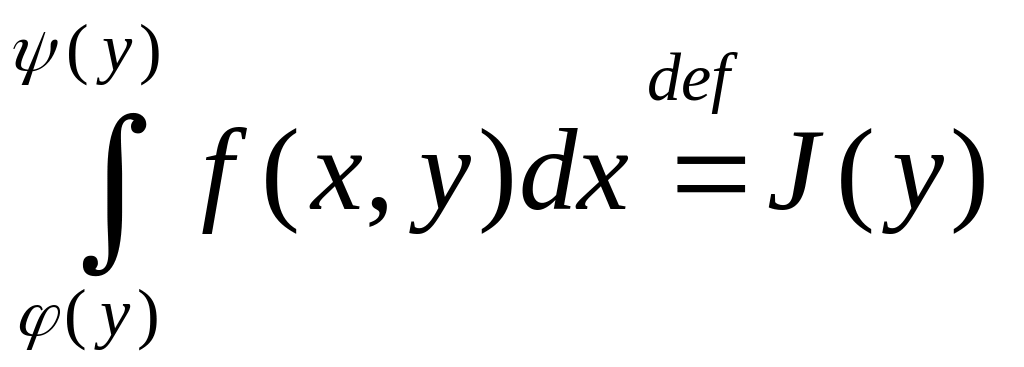 ,
(2)
,
(2)
то этот интеграл называют ИЗОП с переменными границами.
Напомним,
что функция
![]() переменных
переменных
![]() называется равномерно
непрерыв-ной
на
называется равномерно
непрерыв-ной
на
![]() ,
если
,
если
![]() .
.
Теорема 1 (о непрерывности изоп). Если функция непрерывна на прямоугольнике , то изоп есть непрерывная функция на .
□ Поскольку
функция
есть непрерывная на замкнутом
ограниченном
мно-жестве
,
то по
теореме
Кантора
она
является
равномерно непрерывной
на
,
т.е.
![]() .
.
Если взять
![]() ,
то получим
,
то получим
![]() .
(3)
.
(3)
Тогда

Это значит, что
функция
– непрерывна в каждой
точке
![]() .■
.■
Замечание.
Можно
показать, что если
есть непрерывная на
и
![]() – непрерывные
на
,
то
– непрерывные
на
,
то
![]() –
непрерывная
функция на
.
–
непрерывная
функция на
.
Теорема 2 (об интегрируемости изоп). Если функция непрерывна на , то изоп есть интегрируемая на функция, причём
 .
(4)
.
(4)
□ Поскольку
как непрерывная
функция (Теорема 1) является
интегрируемой,
то
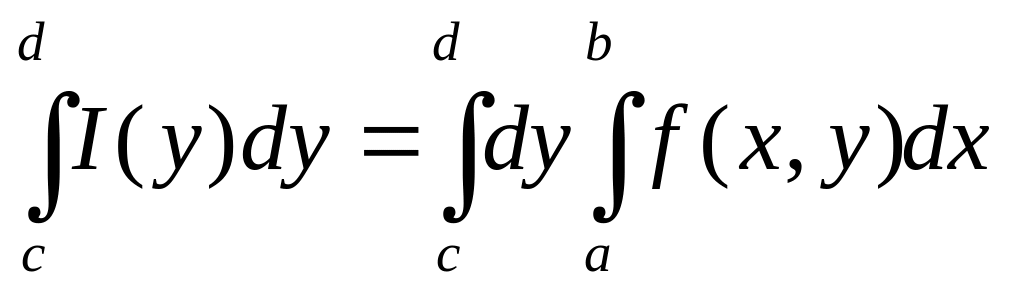 .
Последний
интеграл и интеграл из
правой
части равенства
(4) можно
рассматривать
как
повторные
для двойного
интеграла
.
Последний
интеграл и интеграл из
правой
части равенства
(4) можно
рассматривать
как
повторные
для двойного
интеграла
![]() ,
который
существует для непрерывной
на
функции.
Поэтому интегралы из
(4) совпадают.
■
,
который
существует для непрерывной
на
функции.
Поэтому интегралы из
(4) совпадают.
■
Теорема 3 (о дифференцируемости изоп). Если функция и её частная производная непрерывны на , то изоп есть непрерывно дифференцируемая на функция, причём , (5)
т.е.
 (ИЗОП можно
дифференцировать
под знаком
интеграла).
(ИЗОП можно
дифференцировать
под знаком
интеграла).
□ Введём
вспомогательную
функцию
 .
(6)
.
(6)
Поскольку
 непрерывная на
,
то согласно
теореме
1 функция
непрерывная на
,
то согласно
теореме
1 функция
![]() –
непрерывная
на
–
непрерывная
на
![]() и интеграл от
неё
можно
вычислить
по формуле
(4) интегрирования
ИЗОП под знаком
интеграла:
и интеграл от
неё
можно
вычислить
по формуле
(4) интегрирования
ИЗОП под знаком
интеграла:
 ,
,
т.е.
 ,
откуда
по теореме
Барроу
,
откуда
по теореме
Барроу
![]() .
Заменяя
в (6)
на
.
Заменяя
в (6)
на
![]() ,
получим
(5). ■
,
получим
(5). ■
Формулу (5) называют правилом Лейбница дифференцирования ИЗОП.
Замечание.
Если функции
и
![]() непрерывные
на
и
– непрерывно
дифференцируемые
на
,
то
есть непрерывно
дифференцируемая функция на
,
причём
непрерывные
на
и
– непрерывно
дифференцируемые
на
,
то
есть непрерывно
дифференцируемая функция на
,
причём
 (7)
(7)
– правило Лейбница дифференцирования ИЗОП с переменными границами.
Действительно,
пусть
 .
Тогда
.
Тогда
![]() .
(8)
.
(8)
Функция
![]() имеет непрерывные частные производные
по всем
переменным:
имеет непрерывные частные производные
по всем
переменным:
![]() – согласно
теореме
Барроу;
– согласно
теореме
Барроу;
 –согласно
теореме
3. Тогда из
(8) на основании
теоремы о
производной
сложной
функции
–согласно
теореме
3. Тогда из
(8) на основании
теоремы о
производной
сложной
функции

что и означает справедливость формулы (7).
Пример 1. Вычислить интеграл .
► Будем рассматривать
этот интеграл как
ИЗОП с
параметром
![]() и обозначим
его
через
и обозначим
его
через
![]() =
.
Тогда
=
.
Тогда


Таким образом,
из равенства
 имеем
имеем

Поскольку из
условия
![]()
 следует,
что
следует,
что
![]() ,
то
,
то
![]() .◄
.◄
§10.2. Несобственные интегралы, зависящие от параметра (низоп).
Пусть на полосе
![]() определена функция
.
Если
несобственный интеграл
определена функция
.
Если
несобственный интеграл
 сходится, то говорят, что он
сходится на отрезке
.
При этом на
отрезке
определена функция
сходится, то говорят, что он
сходится на отрезке
.
При этом на
отрезке
определена функция
 ,
(1)
,
(1)
которую называют несобственным интегралом, зависящим от параметра (НИЗОП).
Сходимость НИЗОП к функции означает существование предела
 ,
т.е.
,
т.е.
![]()
 .
.
Таким образом, НИЗОП (1) сходится на отрезке , если и только если
 .
.
def.
Говорят, что НИЗОП (1) сходится равномерно
по параметру
у на отрезке
,
если
![]()
 .
.
Если НИЗОП (1) сходится на отрезке , но не является равномерно сходящимся по параметру на , то говорят, что НИЗОП (1) сходится неравномерно по параметру на отрезке т.е.
![]()
 .
.
