
- •Глава 6. Ряды. §6.1. Свойства сходящихся рядов.
- •Пример 1. Докажем расходимость гармонического ряда, используя определение расходимости числового ряда.
- •Теорема 2. (сходимость линейной комбинации) Если ряды и – сходящиеся соответственно к суммам и , то ряд
- •Теорема 3. Ряд и каждый его остаток либо оба сходятся либо оба расходятся.
- •§6.2. Знакоположительные ряды.
- •Теорема 2. (Дирихле) Если произвольно переставить члены сходящегося знакоположительного ряда, то получится сходящийся ряд, сумма которого равна сумме исходного ряда.
- •Пример 1. Исследуем на сходимость обобщённый гармонический ряд в зависимости от числового параметра .
- •Теорема 4. (Признак сравнения) Если , (6)
- •Пример 2.
- •Теорема 5. ( Предельный признак сравнения ) Пусть и . Тогда ряды и или оба сходятся, или оба расходятся.
- •Пример 3. Пользуясь следствием исследуем на сходимость ряды 1) , 2) .
- •Теорема 6. ( Признак Даламбера ) Если для ряда (1) выполняются условия и , то : 1) при ряд (1) сходится; 2) при ряд (1) расходится.
- •Пример 4.
- •Теорема 7. ( Признак Коши ) Если для ряда (1) выполняются условия и , то : 1) при ряд (1) сходится; 2) при ряд (1) расходится.
- •Пример 5. .
- •§6.3. Знакопеременные ряды.
- •Теорема 2. ( Абеля ) Ряд (1) является сходящимся, если сходится ряд , а последовательность является мнотонной и ограниченной.
- •Теорема 3. ( Признак Лейбница ) Если последовательность монотонно стремится к нулю, то ряд (8) является сходящимся, причём
- •Пример 2. Поскольку , то , а поэтому ряд сходится. §6.4. Абсолютная и условная сходимость ряда.
- •Теорема 1. Пусть ряд является знакопеременным. Если ряд сходится, то и ряд тоже сходится.
- •Теорема 2. При произвольной перестановке слагаемых абсалютно сходящегося знакопеременного ряда получается ряд, сходящийся абсолютно к сумме исходного ряда.
- •Пример. Ряд является условно сходящимся. Пусть – его сумма.
- •Пример 1. .
- •Пример 2. .
- •Пример 3. .
- •Пример 4.
- •Теорема 2. (Критерий Коши рсфр) Для того чтобы функциональный ряд был равномерно сходящимся на множестве , необходимо и достаточно, чтобы выполнялось условие Коши:
- •Теорема 3. ( Признак Вейерштрасса рсфр) Если функциональный ряд имеет на множестве сходящуюся числовую мажоранту, то он равномерно сходится на .
- •1°. Непрерывность суммы ряда.
- •3°. Почленное дифференцирование.
- •1°.Радиус и интервал сходимости.
- •Пример 1. Найти область сходимости степенного ряда .
- •Пример 2. .
- •2°.Свойства степенных рядов. Теорема 3. Степенной ряд сходится равномерно на каждом отрезке, который полностью содержится в его интервале сходимости.
- •Теорема 4. ( Непрерывность суммы степенного ряда ) Сумма степенного ряда является непрерывной функцией на его интервале сходимости.
- •Теорема 5. (Почленное интегрирование степенного ряда) Степенной ряд (1), сходящийся на интервале к сумме , можно почленно интегрировать на каждом отрезке , т.Е. Имеет место равенство
- •Теорема 6. (Почленное дифференцирование степенного ряда) На интервале сходимости степенной ряд можно почленно дифференцировать сколько угодно раз. При этом имеет место равенство
- •Пример 3. Вычислить сумму ряда .
- •§6.8. Ряды Тейлора.
- •1°. Ряд Тейлора .
- •Пример 1. Разложить функцию в ряд Тейлора и найти его сумму.
- •Теорема 1. ( Достаточное условие сходимости ряда Тейлора) Пусть функция является бесконечно дифференцируемой на промежутке и существует число . Тогда ряд Тейлора (2) сходится на к .
- •Теорема 2. (о единственности разложения функции в степенной ряд) Если степенной ряд имеет радиус сходимости , то его коэффициенты выражаются по формуле .
- •4) Степенной бином.
3°. Почленное дифференцирование.
Теорема 3.
(О почленном дифференцировании РСФР)
Если функции
имеют непрерывные производные
![]() на отрезке
,
и ряд
сходится на
к функции
,
а ряд
на отрезке
,
и ряд
сходится на
к функции
,
а ряд
 равномерно сходится на
к функции
равномерно сходится на
к функции
![]() ,
=
,
то
,
=
,
то
![]()
![]() ,
или
,
или
 .
.
□ Согласно теореме
2 равномерно сходящийся
ряд
можно
почленно интегрировать
на отрезке
![]() :
:



Таким образом,
![]() (10)
(10)
Поскольку
функция
непрерывна
на
![]() ,
то по
теореме
Барроу
,
то по
теореме
Барроу
 – дифференцируемая функция. Дифференцируя
равенство
(10),
имеем
– дифференцируемая функция. Дифференцируя
равенство
(10),
имеем
![]() .
■
.
■
Для функциональных последовательностей имеют место аналогичные теоремы.
Теорема 4. Если члены последовательности непрерывны на отрезке , а сама последовательность равномерно сходится на , то её предельная функция тоже непрерывна на отрезке .
Теорема 5. Если члены последовательности непрерывны на отрезке , а сама последовательность равномерно сходится на к предельной функции , то
 .
.
Теорема 6.
Если функции
имеют непрерывные производные
на отрезке
,
и последовательность
сходится на
к функции
,
а последовательность
![]() равномерно сходится на
,
то
–
дифференцируемая
на
и последовательность
имеет предельную функцию
равномерно сходится на
,
то
–
дифференцируемая
на
и последовательность
имеет предельную функцию
![]() ,
т.е.
,
т.е.
![]() .
.
§6.7. Степенные ряды .
1°.Радиус и интервал сходимости.
Функциональный
ряд
 ,
где
,
где
![]() ,
,
![]() – действительная
независимая
переменная,
называется степенным
рядом
с
центром
в
точке
– действительная
независимая
переменная,
называется степенным
рядом
с
центром
в
точке
![]() .
Понятно,
что этот
ряд всегда
сходится в точке
.
Понятно,
что этот
ряд всегда
сходится в точке
![]() .
Если в этом
ряду
сделать
замену переменной
.
Если в этом
ряду
сделать
замену переменной
![]() ,
то полученный
при этом
ряд
,
то полученный
при этом
ряд
 ,
(1)
,
(1)
который будет
далее
объектом
нашего
исследования,
тоже всегда
сходится в точке
![]() .
Может
случиться,
что эта
точка
является единственной
точкой
сходимости
степенного
ряда.
.
Может
случиться,
что эта
точка
является единственной
точкой
сходимости
степенного
ряда.
Пример 1. Найти область сходимости степенного ряда .
При
этот
ряд является сходящимся.
Если
![]() ,
то
,
то
![]() , т.е.
можно
использовать
признак
Даламбера.
Имеем
, т.е.
можно
использовать
признак
Даламбера.
Имеем
 .
.
Это значит, что ряд сходится только при .
В то же время существуют степенные ряды, которые сходятся на всей числовой прямой.
Пример 2. .
При любом
![]() используем
признак
Даламбера
используем
признак
Даламбера
 .
Таким
образом, ряд сходится при всех
.
Таким
образом, ряд сходится при всех
![]() .
.
Теорема 1.
( Абеля )
Если степенной ряд (1)
сходится в некоторой точке
![]() ,
то он абсолютно сходится в каждой точке
,
то он абсолютно сходится в каждой точке
![]() .
Если же этот ряд расходится в некоторой
точке
.
Если же этот ряд расходится в некоторой
точке
![]() ,
то он расходится в каждой точке
,
то он расходится в каждой точке
![]() .
.
□ 1) Пусть ряд (1)
сходится в точке
.
Выберем
произвольно
.
При этом
получим
 .
(2)
.
(2)
Поскольку
числовой
ряд
 сходится,
то
сходится,
то
![]() (необходимое
условие сходимости),
откуда следует
ограниченность
последовательности
(необходимое
условие сходимости),
откуда следует
ограниченность
последовательности
![]() ,
т.е.
,
т.е.
![]() .
(3)
.
(3)
Из
неравенств
(2) и (3) получим
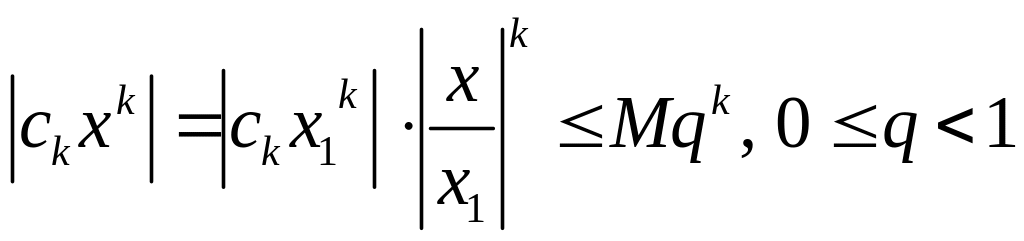 .
(4)
.
(4)
Поскольку
геометрический
ряд
 при
при
![]() является сходящимся,
то по
признаку
сравнения сходится ряд
является сходящимся,
то по
признаку
сравнения сходится ряд
 ,
т.е.ряд (2) сходится при всех
.
,
т.е.ряд (2) сходится при всех
.
2) Пусть ряд (1)
расходится в точке
.
Тогда он
должен
расходиться
в кождой
точке
![]() ,
поскольку
в противном
случае,
согласно
доказанному
выше,
ряд (1) был
бы сходящимся
в точке
.
■
,
поскольку
в противном
случае,
согласно
доказанному
выше,
ряд (1) был
бы сходящимся
в точке
.
■
Теорема 2.
(Об
интервале сходимости)
Если ряд
(1)
сходится более чем в одной точке, но не
на
всей
действительной прямой, то существует
такое действительное число
![]() ,
что ряд (1)
абсолютно сходится на интервале
,
что ряд (1)
абсолютно сходится на интервале
![]() и расходится вне отрезка
и расходится вне отрезка
![]() .
.
□ Пусть
–
область
сходимости
ряда (1). Поскольку
является
непустым
и ограниченным
сверху
множеством
(ряд сходится не на
![]() ),
то существует
),
то существует
![]() .
Покажем,
что ряд (1) сходится на интервале
.
Пусть
.
Покажем,
что ряд (1) сходится на интервале
.
Пусть
![]() – произвольная
точка
интервала
,
т.е.
– произвольная
точка
интервала
,
т.е.
![]() .
Согласно определению
точной
верхней
границы
.
Согласно определению
точной
верхней
границы
![]() .
Поскольку
ряд (1) сходится в
точке
.
Поскольку
ряд (1) сходится в
точке
![]() ,
то по
теореме
Абеля
он
абсолютно
сходится в
точке
.
Таким образом, в
каждой
точке интервала
ряд (1)
абсолютно сходится.
,
то по
теореме
Абеля
он
абсолютно
сходится в
точке
.
Таким образом, в
каждой
точке интервала
ряд (1)
абсолютно сходится.
Если же
лежит
вне
отрезка
,
т.е.
![]() ,
то
,
то
![]() (согласно
определению
точной
верхней
границы),
и поэтому
ряд (1) расходится в точке
.
■
(согласно
определению
точной
верхней
границы),
и поэтому
ряд (1) расходится в точке
.
■
def.
Интервал
,
на котором ряд (1) сходится, а вне отрезка
расходится,
называется интервалом
сходимости
степенного
ряда,
а число
![]() – его
радиусом
сходимости.
– его
радиусом
сходимости.
Замечание 1.
На границе
интервала
сходимости
,
т.е.
в точках
и
![]() ,
ряд (1) может
как
сходиться,
так и расходиться.
,
ряд (1) может
как
сходиться,
так и расходиться.
Замечание 2.
Если степенной
ряд сходится на всей
числовой
прямой,
то говорят,
что радиус
сходимости
этого
ряда
![]() ,
а если ряд сходится только
в точке
,
то
,
а если ряд сходится только
в точке
,
то
![]() .
.
Замечание 3.
Относительно
ряда
доказанная
Теорема
2
приобретает следующее звучание:
степенной
ряд с
центром
в
точке
имеет
интервал
сходимости
![]() ,
где
– радиус
сходимости
этого
ряда,
,
где
– радиус
сходимости
этого
ряда,
![]() .
.
Для нахождения радиуса сходимости степенного ряда можно использовать прикзнаки Даламбера или Коши.
1)
Формула Даламбера.
Пусть существует
конечный
 .
Тогда
.
Тогда
 .
.
Согласно предельному
признаку
Даламбера ряд (1) сходится абсолютно,
если
![]() ,
и расходится при
,
и расходится при
![]() .
Таким образом, в
точках сходимости
выполняется
неравенство
.
Таким образом, в
точках сходимости
выполняется
неравенство
![]() ,
а в точктах расходимости
,
а в точктах расходимости
![]() .
Отсюда
получаем,
что радиус
сходимости
равен
.
Отсюда
получаем,
что радиус
сходимости
равен
![]() ,
или
,
или
 .
(5)
.
(5)
2) Формула Коши. Аналогично при помощи предельного признака Коши получается формула Коши для нахождения радиуса сходимости степенногоага ряда ( при условии существования соответствующего предела ):
 .
(6)
.
(6)
Случаи
 ,
или
,
или
![]() соответствуют
значению
.
соответствуют
значению
.
Если же
получается бясконечный
предел
![]() ,
то это
соответствует значению
,
что означает
сходимость
степенного
ряда
только
в точке
.
,
то это
соответствует значению
,
что означает
сходимость
степенного
ряда
только
в точке
.
