
- •Глава 6. Ряды. §6.1. Свойства сходящихся рядов.
- •Пример 1. Докажем расходимость гармонического ряда, используя определение расходимости числового ряда.
- •Теорема 2. (сходимость линейной комбинации) Если ряды и – сходящиеся соответственно к суммам и , то ряд
- •Теорема 3. Ряд и каждый его остаток либо оба сходятся либо оба расходятся.
- •§6.2. Знакоположительные ряды.
- •Теорема 2. (Дирихле) Если произвольно переставить члены сходящегося знакоположительного ряда, то получится сходящийся ряд, сумма которого равна сумме исходного ряда.
- •Пример 1. Исследуем на сходимость обобщённый гармонический ряд в зависимости от числового параметра .
- •Теорема 4. (Признак сравнения) Если , (6)
- •Пример 2.
- •Теорема 5. ( Предельный признак сравнения ) Пусть и . Тогда ряды и или оба сходятся, или оба расходятся.
- •Пример 3. Пользуясь следствием исследуем на сходимость ряды 1) , 2) .
- •Теорема 6. ( Признак Даламбера ) Если для ряда (1) выполняются условия и , то : 1) при ряд (1) сходится; 2) при ряд (1) расходится.
- •Пример 4.
- •Теорема 7. ( Признак Коши ) Если для ряда (1) выполняются условия и , то : 1) при ряд (1) сходится; 2) при ряд (1) расходится.
- •Пример 5. .
- •§6.3. Знакопеременные ряды.
- •Теорема 2. ( Абеля ) Ряд (1) является сходящимся, если сходится ряд , а последовательность является мнотонной и ограниченной.
- •Теорема 3. ( Признак Лейбница ) Если последовательность монотонно стремится к нулю, то ряд (8) является сходящимся, причём
- •Пример 2. Поскольку , то , а поэтому ряд сходится. §6.4. Абсолютная и условная сходимость ряда.
- •Теорема 1. Пусть ряд является знакопеременным. Если ряд сходится, то и ряд тоже сходится.
- •Теорема 2. При произвольной перестановке слагаемых абсалютно сходящегося знакопеременного ряда получается ряд, сходящийся абсолютно к сумме исходного ряда.
- •Пример. Ряд является условно сходящимся. Пусть – его сумма.
- •Пример 1. .
- •Пример 2. .
- •Пример 3. .
- •Пример 4.
- •Теорема 2. (Критерий Коши рсфр) Для того чтобы функциональный ряд был равномерно сходящимся на множестве , необходимо и достаточно, чтобы выполнялось условие Коши:
- •Теорема 3. ( Признак Вейерштрасса рсфр) Если функциональный ряд имеет на множестве сходящуюся числовую мажоранту, то он равномерно сходится на .
- •1°. Непрерывность суммы ряда.
- •3°. Почленное дифференцирование.
- •1°.Радиус и интервал сходимости.
- •Пример 1. Найти область сходимости степенного ряда .
- •Пример 2. .
- •2°.Свойства степенных рядов. Теорема 3. Степенной ряд сходится равномерно на каждом отрезке, который полностью содержится в его интервале сходимости.
- •Теорема 4. ( Непрерывность суммы степенного ряда ) Сумма степенного ряда является непрерывной функцией на его интервале сходимости.
- •Теорема 5. (Почленное интегрирование степенного ряда) Степенной ряд (1), сходящийся на интервале к сумме , можно почленно интегрировать на каждом отрезке , т.Е. Имеет место равенство
- •Теорема 6. (Почленное дифференцирование степенного ряда) На интервале сходимости степенной ряд можно почленно дифференцировать сколько угодно раз. При этом имеет место равенство
- •Пример 3. Вычислить сумму ряда .
- •§6.8. Ряды Тейлора.
- •1°. Ряд Тейлора .
- •Пример 1. Разложить функцию в ряд Тейлора и найти его сумму.
- •Теорема 1. ( Достаточное условие сходимости ряда Тейлора) Пусть функция является бесконечно дифференцируемой на промежутке и существует число . Тогда ряд Тейлора (2) сходится на к .
- •Теорема 2. (о единственности разложения функции в степенной ряд) Если степенной ряд имеет радиус сходимости , то его коэффициенты выражаются по формуле .
- •4) Степенной бином.
Пример 3. Вычислить сумму ряда .
Вычислим
сначала
радиус сходимости
этого
ряда.
 .
.
Это
значит,
что ряд сходится на интервале
![]() к
некоторай
сумме
к
некоторай
сумме
 .
На основании
теоремы 6 имеем
.
На основании
теоремы 6 имеем
 (геометрический
ряд). Интегрируя
это
ровенство,
имеем
(геометрический
ряд). Интегрируя
это
ровенство,
имеем
![]() .
Поскольку
.
Поскольку
![]()
 ,
то из
равенства
,
то из
равенства
![]() получаем,
что
получаем,
что
![]() .
Таким образом,
.
Таким образом,
 .
.
§6.8. Ряды Тейлора.
1°. Ряд Тейлора .
Пусть функция
является бесконечно дифференцируемой
на промежутке
![]() ,
т.е.
имеет
производные любога порядка.
Тогда
,
т.е.
имеет
производные любога порядка.
Тогда
![]() и
и
![]() имеет
место
формула Тейлора
имеет
место
формула Тейлора
 .
(1)
.
(1)
def.
Степенной
ряд
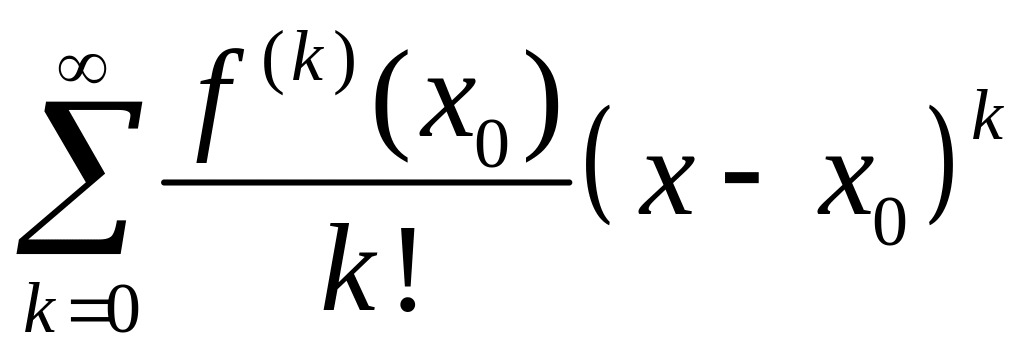 (2)
(2)
называется рядом
Тейлора
для бесконечно дифференцируемой
на промежутке
функции
.
Если
![]() ,
то ряд Тейлора называется рядом
Маклорена.
,
то ряд Тейлора называется рядом
Маклорена.
Согласно формуле
(1) ряд Тейлора (2) сходится к
функции
в
точке
![]() ,
если и тольки если
,
если и тольки если
![]() .
(3)
.
(3)
( В этом случае последовательность частичных сумм ряда (2) стремится к функции .)
Замечание. Существование производных любого порядка недостаточно для того, чтобы ряд Тейлора сходился к той же функции, для которой он построен.
Пример 1. Разложить функцию в ряд Тейлора и найти его сумму.
Понятно, что при функция бесконечно дифференцируемая. Вычислим её производную в точке :
 .
.
Аналогично
получаются
производные
![]() .
Таким образом, ряд Маклорена для функции
является
.
Таким образом, ряд Маклорена для функции
является
 .
.
Теорема 1. ( Достаточное условие сходимости ряда Тейлора) Пусть функция является бесконечно дифференцируемой на промежутке и существует число . Тогда ряд Тейлора (2) сходится на к .
□ Достаточно
показать,
что при выполнении
условий
теоремы выполняется
условие
(3). Запишемм
остаточный
член
формулы Тейлора в форме Лагранжа
 .
Можно считать, что
.
Можно считать, что
![]() ,
а поэтому
,
а поэтому
![]() .
Поскольку
.
Поскольку
![]() ,
то
,
то
 .
(4)
.
(4)
Как
мы знаем,
 ,
поэтому
,
поэтому
![]()
 .
(5)
.
(5)
Из (4) и (5) следует, что . ■
Теорема 2. (о единственности разложения функции в степенной ряд) Если степенной ряд имеет радиус сходимости , то его коэффициенты выражаются по формуле .
□ Дифференцируя
равенство
![]()
раз (это возможно на основании теоремы 6 §6.7.), получим
![]() .
.
Взяв
в последнем
равенстве
,
получим
 .
Эта означает,
что степенной
ряд на интервале
его
сходимости
является
рядом
Тейлора для своей
суммы.
■
.
Эта означает,
что степенной
ряд на интервале
его
сходимости
является
рядом
Тейлора для своей
суммы.
■
2°. Ряды Маклорена для некаторых элементарных функций.
Для получения
разложения
основных
элементарных функций по формуле
Маклорена
 (6)
(6)
будем использовать наработки, сделанные нами в §5.2.
1) Экспонента и гиперболические функции.
Поскольку
для функции
![]()
![]() ,
то на каждом
интервале
,
то на каждом
интервале
![]() имеют
место
неравенства
имеют
место
неравенства
![]() .
Согласно
следствиею
из
теоремы 1 ряд (6) сходится к
функции
.
Согласно
следствиею
из
теоремы 1 ряд (6) сходится к
функции
![]() на интервале
на интервале
![]() ,
т.е.
радиус
сходимости
этого
ряда
,
т.е.
радиус
сходимости
этого
ряда
![]() .
Таким образом, имеет
место
формула
.
Таким образом, имеет
место
формула
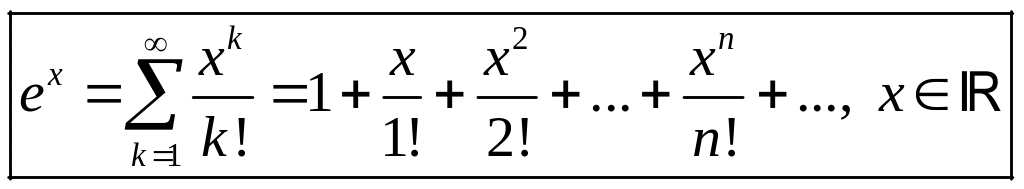 .
(7)
.
(7)
Используя
равенство
(7) и формулы
![]() ,
получаем
разложения
функций
,
получаем
разложения
функций
![]() и
и
![]() в
ряд Маклорена:
в
ряд Маклорена:
 .
.
2) Тригонометрические функции.
Поскольку
функция
![]() является бесконечно дифференцируемой
на всей
числовой
прямой,
а для яе производных
является бесконечно дифференцируемой
на всей
числовой
прямой,
а для яе производных
 ,
то васоответствии
со следствиеем
из
теоремы 1, ряд (6) для функции
сходится к
этой
функции на всей
числовой
прямой,
и при этом
имеет
место
формула
,
то васоответствии
со следствиеем
из
теоремы 1, ряд (6) для функции
сходится к
этой
функции на всей
числовой
прямой,
и при этом
имеет
место
формула
 .
.
Аналогично
получается формула
 .
.
3) Логарифмическая функция.
В
примере
3 §6.7.
мы получили,
что
.
Если в этом
равенстве
заменить
на
![]() ,
то получим
,
то получим
 .
.
Согласно Теореме
2, это
равенство
даёт
разложение
функции
![]() по
формуле
Маклорена на интервале
.
При этом
при
по
формуле
Маклорена на интервале
.
При этом
при
![]() получается тоже сходящийся
ряд
получается тоже сходящийся
ряд
 .
Таким образом, имеем формулу
.
Таким образом, имеем формулу
 .
(8)
.
(8)
При
,
В частностиполучается
 .
.
Замечание.
Пользуясь
признаком
Даламбера, можно
показать,
что при
![]() ряд (8) расходится.
При
он
тоже расходится как
гармонический. Таким образом, хотя
функция
определена
на промежутке
ряд (8) расходится.
При
он
тоже расходится как
гармонический. Таким образом, хотя
функция
определена
на промежутке
![]() ,
разложение
(8) имеет
место
только
при
,
разложение
(8) имеет
место
только
при
![]() .
.
