4. Определение надёжности производственных систем
Допустим, что производственная система S состоит из n элементов е1, е2, …, еn. Надёжности элементов (вероятности безотказной работы) известны р1, р2, …, рn. Для безотказной работы системы, состоящей из нескольких последовательно соединённых элементов (например станков, объединённых в технологическую линию), нужно, чтобы работал безотказно каждый из её элементов. Тогда по правилу умножения вероятностей независимых событий надёжность Р системы равна
Рис. 6. Система из последовательно соединённых
элементов
Задача. Определить надёжность системы, состоящей из десяти последовательно соединённых элементов, надёжность каждого из которых равна р = 0,95. Поскольку вероятности безотказной работы для всех элементов одинаковы, то вместо произведения используем возведение в степень
Р = рn = 0,9510 ≈ 0,6.
Одним из путей повышения надёжности системы является резервирование её элементов. При этом дублирующие элементы включаются в систему параллельно тем, надёжность которых недостаточна. В этом случае надёжность Р системы определяется из выражения
.
Рис. 7. Система из параллельно соединённых элементов
Задача. Определить надёжность системы, состоящей из трёх дублирующих друг друга элементов, надёжность каждого из которых составляет р = 0,9. Поскольку вероятности безотказной работы для всех элементов одинаковы, то вместо произведения используем возведение в степень
Р = 1 – (1 – 0,9)3 = 0,999.
Задание. Определить надёжность системы, представленной на рис. 8.
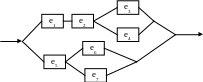
Рис. 8. Производственная система из семи элементов
Варианты вероятностей безотказной работы элементов
Варианты |
е1 |
е2 |
е3 |
е4 |
е5 |
е6 |
е7 |
1 |
0,95 |
0,9 |
0,85 |
0,8 |
0,75 |
0,7 |
0,75 |
2 |
0,9 |
0,85 |
0,8 |
0,75 |
0,7 |
0,75 |
0,8 |
3 |
0,85 |
0,8 |
0,75 |
0,7 |
0,75 |
0,8 |
0,85 |
4 |
0,8 |
0,75 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
5 |
0,75 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
6 |
0,7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
0,9 |
7 |
0,75 |
0,8 |
0,85 |
0,9 |
0,95 |
0,9 |
0,85 |
8 |
0,8 |
0,85 |
0,9 |
0,95 |
0,9 |
0,85 |
0,8 |
9 |
0,85 |
0,9 |
0,95 |
0,9 |
0,85 |
0,8 |
0,75 |
10 |
0,9 |
0,95 |
0,9 |
0,85 |
0,8 |
0,75 |
0,7 |
ПРОГРАММА ДИСЦИПЛИНЫ
"Методы моделирования производственных систем"