54. Барометрическая формула.

Давление на высоте h+dh будет p+dp, причем если dh >0, то dp < 0, так как вес вышележащих слоев атмосферы, а следовательно и давление с высотой убывают.Разность давления: p-(p+dp)= ρgdh, где ρ-плотность газа на высоте h,=> dp=- ρgdh. dp=-(Mg)/(RT)dh. T=const => lnp=-(Mgh)/(RT)+lnC, p=C exp(-(Mgh)/(RT)),подставим h=0,получим что C=p_o,=> p=p₀ exp(-(Mgh)/(RT)) эта формула наз. Бараметрической. Из нее следует, что давление убывает с высотой тем быстрее, чем тяжелее газ и чем ниже температура.

28. Опыт Майкельсона и Морли.

В классической механике v<<c . С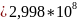 . В СТО рассматриваются случаи, когда v~c. Тогда считалось, что в пространстве эфир.

Опыты Майкельсона и Морли являются независимыми от 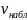или источника.

Опыт: Пусть на жёстком основании длиной D имеется источник света и отражающее зеркало. 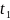-> вправо 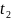обратно. 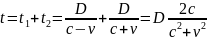Теперь повернём установку на угол .

; ; ;

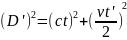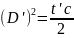Подставляем. Получаем: ;

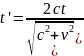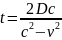; Считаем t’. Считаем t-t’=…= .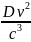

Замедление времени.t – время, за которое луч достиг до зеркала.А и В – 2 часов. На В есть кисточка. Когда В проходит через А, оставляет метку. Если метка на краю, то нет изменений. Если ниже, то В уменьшились. Наблюдатель, движущийся с А, увидит, что движущиеся световые часы стали короче. А с точки зрения наблюдателя за В движущиеся относительно него часы окажутся длиннее. Но по принципу ТО наблюдатели равноправны. Далее рассмотрим систему с точки зрения наблюдателя, покоящегося в системе А. Для него пусть свет луча будет представляться более длинным, чем в часах А.

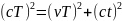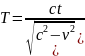; ;Этот наблюдатель видит: часы тикают реже t.Пусть есть механические и световые часы. Помещаем механические часы в движущуюся систему. Видим: световые отстали, механические не меняются.

51.Наиболее вероятная скорость молекул.Наиболее вероятная скорость молекул — это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул Данная формула вытекает из распределения Максвелла. Наиболее вероятная скорость, как показал он, зависит от температуры газа и массы молекул.Что бы получить из первой формулы скорости молекулы вторую, надо сделать всего две замены, расписать универсальную газовую постоянную, как R=N_ak, и молярную массу.M=N_am , то у нас получится из этой формулы: V— Наиболее вероятная скорость молекул.K=1,38*10^-23 — Постоянная Больцмана.T — Температура.m — Масса одной молекулы.R=8,31— Универсальная газовая постоянная M— Молярная масса. v— Количество вещества.N_a=6,02*10²³ — Число Авогадро

30. Движение твердого тела. Расчет кинетической энергии.

Плоское движение твердого тела – это такое движение, при котором траектории всех точек тела лежат в параллельных плоскостях. Когда тело вращается, то ось вращения сохраняет свою ориентацию в протран-стве и остается перпендикулярной плоскости, в которой движется центр масс.Плоское движение твердого тела в данный момент времени можно представить как чисто вращательное движение вокруг мгновенной оси вращения, проходящей через неподвижную точку, скорость v которой равна нулю в неподвижной лабораторной системе отсчета, жестко связанной с Землей.Уравнения плоского движения твердого тела:1. Уравнение движения центра масс, определяющее скорость поступательного движения тела массой т:mdv_c/dt=(сумм)i F_i, где v_c– скорость центра масс тела; (сумм)i F_i – сумма всех внешних сил.2. Уравнение динамики плоского движения относительно оси, проходящей через центр масс тела и неподвижной относительно тела, определяющее угловую скорость w_c вращательного движения: I_cdw_c/dt=^внешн.M_c, где I_c и ^внешн.M_c – момент инерции тела и момент внешних сил относительноэтой оси соответственно.оси соответственно.Кинетическая энергия тела, совершающего плоское движение. Если рассматривать движение тела как вращение вокруг мгновенной оси, то элемент массы 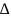m_i имеет в данный момент времени линейную корость v_i = wr_i , где r_i – расстояние от этого элемента до мгновенной оси. Кинетическая энергия отдельного элемента тела будет: E_ki= m_iv²_i= mir2iw2, а кинетическая энергия всего тела: E_k=(сумм) E_ki=w²/2(сумм) m_ir²_i=Iw²/2, где I – момент инерции тела относительно мгновенной оси.Теорема Кёнига:полная кинетическая энергия при плоском движении твердого тела равна сумме кинетических энергий поступательного и вращательного движений (вращение рассматривается вокруг оси, проходящей через центр масс).