
- •16/Закон всемирного тяготения. Космические скорости
- •15Диамика материальной точки. Законы Ньютона.
- •3/Принцип относительности Галилея: все механические явления в различных инерциальная система отсчёта
- •2/Средняя скорость, среднее по времени.
- •7/Эффект допплера
- •13/Импульс. Реактивное движение
- •20/Кеплерово движение. Третий закон Кеплера.
- •12/Вращательный момент. Основное уравнение.
- •11/Закон сохранения энергии. Внутренняя энергия.
- •21/Момент импульса. /Его сохранение
- •23/Движение в центральном поле сил.
- •31/Момент инерции.
- •39/Затухающие колебания.
- •30/Движение твёрдого тела.
- •9.Неинерциальные системы отсчета. Сила кориолиса
- •8.Волны. Энергия упругих волн. Вектор умова.
- •5.Скорость распространения волн. Скорость звука.
- •37/ Теорема Штейнера и ее использование.
- •45/Идеальный газ и его законы.
- •44/Предмет и методы молекулярной физики.
- •56. Работа при изопроцессах.
- •54. Барометрическая формула.
- •28. Опыт Майкельсона и Морли.
- •30. Движение твердого тела. Расчет кинетической энергии.
- •48.Теоремы сложения и умножения вероятностей. Нормировка.
- •18. Потенциальная энергия вне и внутри шара для точечной массы.
- •19. Движение в однородном поле.
- •50.Распределение молекул по координатам.
- •34. Энергия гармонических колебаний.
- •52.Распределение Максвелла в сферических координатах.
- •49. Распределение по вектору скоростиУчитывая, что плотность распределения по скоростям пропорциональна плотности распределения по импульсам: и используя мы получим:
23/Движение в центральном поле сил.
Пусть
частица массы m движется в центральном
силовом поле. Момент сил, действующих
на частицу
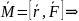 момент импульса частицы
момент импульса частицы
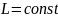 .
В силу сохранения
.
В силу сохранения
 ,
направление движения частицы должно
происходить перпендикулярно направлению
.
Частица совершает плоское движение.
Для описания движения воспользуемся
полярной системой координат:
,
направление движения частицы должно
происходить перпендикулярно направлению
.
Частица совершает плоское движение.
Для описания движения воспользуемся
полярной системой координат:
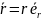 ,
,
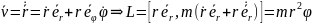 – проекция моментов на ось Z сохраняется.
Т.к. силовое поле является центральным,
то оно консервативное, значит, для него
можно найти выражение для потенциальной
энергии U. При движении в консервативном
силовом поле сохраняется полная
механическая энергия.
– проекция моментов на ось Z сохраняется.
Т.к. силовое поле является центральным,
то оно консервативное, значит, для него
можно найти выражение для потенциальной
энергии U. При движении в консервативном
силовом поле сохраняется полная
механическая энергия.
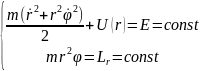 , таким образом, задача по движению
частицы в центральном силовом поле
свелась к решению системы 2-ух
дифференциальных уравнений 1-ого
порядка. При этом мы используем момент
энергии и момент сил.
, таким образом, задача по движению
частицы в центральном силовом поле
свелась к решению системы 2-ух
дифференциальных уравнений 1-ого
порядка. При этом мы используем момент
энергии и момент сил.
31/Момент инерции.
Момент
инерции
определяется как
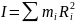 ,
если распределение массы равномерно,
то
,
если распределение массы равномерно,
то
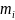 заменяется на
заменяется на
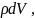
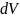 – элементарный объём,
– элементарный объём,
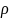 – плотность вещества.
– плотность вещества.
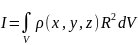 .
.
Момент инерции:
однородного тонкого стержня массы
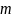 ,
длины
,
длины
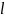 относительно оси, проходящей через
центр масс и перпендикулярной стержню:
относительно оси, проходящей через
центр масс и перпендикулярной стержню: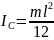
однородного тонкого стержня массы , длины относительно оси, проходящей через один из концов стержня:
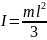
тонкого кольца массы , радиуса R относительно оси симметрии, перпендикулярной плоскости кольца:
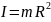
однородного диска (цилиндра) массы , радиуса R, высоты h относительно оси симметрии, перпендикулярной основанию:
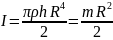 .
.
39/Затухающие колебания.
В
реальных физических системах всегда
действуют силы сопротивления, в
результате действия которых амплитуда
колебаний с течением времени убывает.
рассмотрим движение тела в вязкой
среде, когда силы сопротивления
противоположны скорости движения тела:
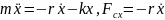 ,
,
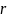 –
коэффициент сопротивления.
–
коэффициент сопротивления.
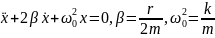 .
Подставим вместо
.
Подставим вместо
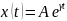 – дифференциальное уравнение 2-ого
порядка сводится к квадратному
алгебраическому уравнению
– дифференциальное уравнение 2-ого
порядка сводится к квадратному
алгебраическому уравнению
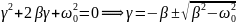 .
Колебательный процесс возможен, если
силы сопротивления достаточно малы.
Это означает, что должно выполняться
условие
.
Колебательный процесс возможен, если
силы сопротивления достаточно малы.
Это означает, что должно выполняться
условие
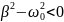 .
В этом случае
.
В этом случае
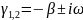 .
Следовательно, общим решением нашего
уравнения будет функция
.
Следовательно, общим решением нашего
уравнения будет функция
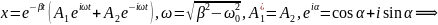
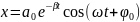 – кинематический закон затухающих
колебаний. Можно сказать, что наблюдаются
гармонические колебания с частотой
– кинематический закон затухающих
колебаний. Можно сказать, что наблюдаются
гармонические колебания с частотой
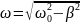 ,
амплитуда же колебаний убывает по
экспоненциальному закону
,
амплитуда же колебаний убывает по
экспоненциальному закону
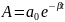 .
Скорость затухания определяется
величиной коэффициента затухания
.
Скорость затухания определяется
величиной коэффициента затухания
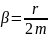 .
Затухание характеризуется также
декрементом затухания, который показывает
во сколько раз уменьшилась амплитуда
колебаний за время, равное периоду
.
Затухание характеризуется также
декрементом затухания, который показывает
во сколько раз уменьшилась амплитуда
колебаний за время, равное периоду
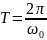 :
:
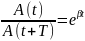 .
Логарифм этого выражения называют
логарифмическим декрементом затухания:
.
Логарифм этого выражения называют
логарифмическим декрементом затухания:
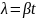 .
В затухающих системах используется
также такая величина как добротность:
.
В затухающих системах используется
также такая величина как добротность:
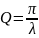 .
.
40/Вынужденными
называются такие колебания,
которые возникают в колебательной
системе под действием внешней периодически
изменяющейся силы (вынуждающая сила).
Пусть вынуждающая сила меняется по
гармоническому закону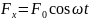 .
С учётом сил сопротивления и упругости
получим динамическое уравнение движения
системы:
.
С учётом сил сопротивления и упругости
получим динамическое уравнение движения
системы:
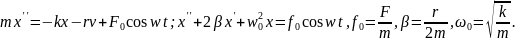 Предположим, что система совершает
гармонические колебания с частотой
Предположим, что система совершает
гармонические колебания с частотой
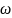 ,
отставая по фазе от вынуждающей силы
на
,
отставая по фазе от вынуждающей силы
на

 .
Находим 1-ую и 2-ую производные и
подставляем в динамическое уравнение
движения системы:
.
Находим 1-ую и 2-ую производные и
подставляем в динамическое уравнение
движения системы:
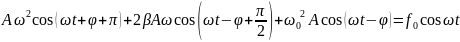 .
В левой части стоит сумма 3-х колебаний
одинаковой частоты, сдвинутой по фазе
и с различными амплитудами. При
.
В левой части стоит сумма 3-х колебаний
одинаковой частоты, сдвинутой по фазе
и с различными амплитудами. При
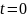 фаза результирующих колебаний должна
равняться 0. С помощью векторной диаграммы
определили амплитуду результирующих
колебаний
фаза результирующих колебаний должна
равняться 0. С помощью векторной диаграммы
определили амплитуду результирующих
колебаний
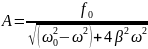 .
.
Начальная
фаза
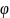 определена условием:
определена условием:
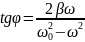 .
.
При
некоторой определённой для данной
системы частоте
,
амплитуда достигает максимального
значения. Колебательная система
оказывается особенно отзывчивой на
действие вынуждающей силы при этой
частоте. Это явление называется
резонансом, а частота – резонансной
частотой.
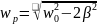 ,
,
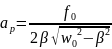 .
.
10.РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. F=-gradU.
Рассмотрим
движение материальной точки в некотором
силовом поле F.
Если под действием силы F
материальная точка прошла dS.
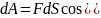 ,dS)
- работа
силы F
на пути dS.
Для того, чтобы определить А сил поля,
не на бесконечно-малом, а на конечном
пути, нужно разбить этот путь на
бесконечно-малые участки dS.Работа
сил поля при переносе частиц из одной
точки в другую не зависит от траектории,
а определяется лишь положением начальной
и конечной точек. Величина U,
т.е. взятая с обратным знаком A
при переходе частицы из точки О в точку
Р называют потенциальной энергией
частицы в точке Р. Работа силового поля
А12 при переходе тела из точки А12=U1-U2,
где U1
и U2
значения потенциальной энергии в этих
точках.dA=-dU;
dA=FdS;
F=-dU/dS;В
общем случае:F=-gradU
,dS)
- работа
силы F
на пути dS.
Для того, чтобы определить А сил поля,
не на бесконечно-малом, а на конечном
пути, нужно разбить этот путь на
бесконечно-малые участки dS.Работа
сил поля при переносе частиц из одной
точки в другую не зависит от траектории,
а определяется лишь положением начальной
и конечной точек. Величина U,
т.е. взятая с обратным знаком A
при переходе частицы из точки О в точку
Р называют потенциальной энергией
частицы в точке Р. Работа силового поля
А12 при переходе тела из точки А12=U1-U2,
где U1
и U2
значения потенциальной энергии в этих
точках.dA=-dU;
dA=FdS;
F=-dU/dS;В
общем случае:F=-gradU
