57. Представление модели экономического роста Солоу с разбиением капитала на физический и человеческий.

В рассмотренной Баумолем модели количества труда, капитала и земли определяют выпуск при убывающей доходности первых двух видов затрат. Тогда превышение выпуска над дифференциальной рентой и минимально необходимой (но не фактической) зарплатой будут определять накопление капитала и рост народонаселения.

В этом механизме существенную роль играет следующая производственная связь:

где Y, L, K, R соответственно совокупный выпуск, труд, капитал, используемая земля;

A(t) - рост производительности за счет экзогенных инноваций.

Г. Мэнкью, Д. Ромер и Д. Уэйл в расширенной модели Солоу, разделяя капитал на физический и человеческий, ввели производственную функцию:

где -H(t)- человеческий капитал.

Для высокоразвитых стран:

Для среднразвитых стран:

Из формул следует, что в целом уровень развития человеческого капитала выше, чем уровень развития физического капитала.

58. Схема функционирования автоматического саморегулятора в цепи обратной связи

Системы автомат-го регулир-я (стабилизации), ведут свое начало от регулятора Уатта, созданного для автомат-й стабилизации числа оборотов выходного вала паровой машины (при изменяющейся внешней нагрузке на вал). Принцип, заложенный в этот регулятор, присущ всем системам автомат-й стабилизации в технике, в живых организмах (поддержание температуры тела др.).

В таких системах требуемое постоянное значение выходной переменной задается настройкой регулятора. Для осуществления процесса регулирования необходимы по крайней мере три основных блока: измерительный (Изм.), регулятор (РБ) и исполнительный (Исп.), расположенные в цепи обратной связи, присоединенной к объекту регулирования (ОР).

Измерит-ый блок служит для измерения фактич-го значения выходной перем-й OP y(t) и ее преобразования в сигнал, удобный для передачи в орган управления. Простейший РБ осуществляет сравнение двух величии - y₀ которая определяется настройкой регулятора, и y(t) и вырабатывает сигнал ,который с обратным знаком поступает в Исп. Если мощность этого сигнала недостаточна для приведения в действие Исп., то в цепь включают усилитель мощности. Исполнительный блок воздействует на вход управляемого объекта, увеличивая или уменьшая его интенсивность до величины, обеспечивающей требуемое значение выходной переменной.

59. Алгоритм численного решения модели динамического моБа и экономическое содержание его параметров

1. Простейшая динамич. модель МОБа с пост-ми коэфф-ми выглядит так:

, (1)

- в-р-ст-ц объемов производства в году t ( );

- в-р-ст-ц абсол-х приростов произв-ва в году t (в-р-ст-ц производных функций);

- в-р-ст-ц потребл-я (включая непроизводств. потреблен-ие) в году t;

- матрица коэфф-ов прямых материал-х затрат;

- матрица коэфф-ов капиталоемкости приростов произв-ва.

_2. Неоднородная система дифф-х уравн-й (1) эквивалентна системе:

, (2)

где - в-р-ст-ц конечн. использ-я продукции отраслей в году t, ( );

- в-р-ст-ц абсол-х приростов конечной продукции по отраслям.

3. Матрица А продуктивна или неразложима, матрица F невырожденна , (поэлементно).

4.Решения системы (2) при в силу неотрицательности матриц и гарантируют, что , , .

5. Динам. модель замкнутой производственно – эконом. системы, представляющейсобой линейную однород. систему дифф.х уравн.й выглядит так

(3)

Решение системы (3) характ-т предельные технолог-е возможн-ти развития производства при задан. матрицах А и F, когда все ресурсы ВВП направляются на расширенное воспроизводство.

6. Общее решение системы (3) имеет следующий аналитический вид:

(4)

Параметры аналит-го решения (4) , , получаются в след. последовательности:

a) - корни характеристического уравнения n-го порядка.

(5)

б) - соответствующие собственные векторы матрицы , , и являются решениями (бесконечными) алгебраич-й системы однородных уравнений: , (6)

где, 0 (“нуль”) – нулевой вектор – столбец размерности ;

в) - постоянные, определяемые из системы уравнений: (7)

где, Y(0) – в-р–с-ц конечн. использ-я продукции отраслей в базисном году.

В общем случае решение (7) содержит несколько отл-х от нуля компонент . Поэтому, единств. траектория системы (3), выходящая из начальной точки Y(0), представляет собой комбинацию экспонент, растущих с различными темпами.

7. Пусть 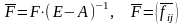. (где F - матрица коэфф-ов капиталоемкости приростов произв-ва.)

Для матрицы существует теорема Перрона:

а) матрица имеет положительное собственное число , которое превосходит модули всех остальных собственных чисел;

б) для , называемого корнем Фробениуса – Перрона, выполняется условие:

.

в) собственному числу отвечает единственный собственный вектор , все координаты которого строго положительны и удовлетворяют условию:

8. Так как , , - соответствует вектор .

9. Значение в межотраслевой динамической модели находит объяснение технологического темпа прироста ВВП, а вектор - отраслевой структуры ВВП.