27. Уравнение Бернули.

Уравнение Бернулли.

Если n = 1, то это – уравнение с разделяющимися переменными, если n = 0, то это – линейное уравнение.

Заметим, что при n > 0 - решение уравнения.

Решать уравнение Бернулли можно тремя способами

1) сведение к линейному уравнению заменой

Разделим обе части уравнения на ,

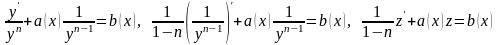
Получили линейное уравнение относительно .

Этот метод применяется редко, так как уравнение Бернулли можно решать теми же методами, что и линейное уравнение, не приводя его предварительно к линейному.

2) Решение методом вариации произвольной постоянной.

Решение проводится аналогично линейному уравнению.

Решим сначала однородное уравнение, полагая правую часть уравнения нулевой.

.

Затем ищем решение уравнения в виде , варьируя произвольную постоянную ,

вычисляем и подставляем в исходное уравнение .

.

Вновь, как и в линейном уравнении, два слагаемых сокращаются, получаем уравнение с разделяющимися переменными.

Определяя отсюда функцию , подставляем ее в .

3)Решение методом подстановки.

Полагаем , подставляем в исходное уравнение

.

Точно так же, как при решении линейного уравнения, решаем, например, уравнение . Подставляем полученную функцию, решаем «оставшееся» уравнение с разделяющимися переменными .

Заметим, что оно получилось точно таким же, как в методе вариации. Поэтому вторая функция в методе подстановки и есть та самая варьируемая постоянная. Затем записываем решение .

Видим, что метод вариации и метод подстановки, фактически, один и тот же метод. Просто в методе подстановки с самого начала используется то, что решение представляется в виде произведения двух функций независимой переменной.

Пример.

Решим это уравнение Бернулли методом вариации произвольной постоянной.

,

,

28. Понятие дифференциального уравнения второго порядка и его решение

   Уравнение вида y''+ρy'+qy=f(x), где ρ и q – вещественные числа, f(x) – непрерывная функция, называется линейным дифференциальным уравнением с постоянными коэффициентами.      Рассмотрим линейное уравнение второго порядка вида:       y''+ρy'+qy=0,                                                      (1)      у которого правая часть f(x) равна нулю. Такое уравнение называется однородным.      Уравнение      K²+ρK+q=0                                             (2)      называется характеристическим уравнением данного уравнения (1).      Характеристическое уравнение (2) является квадратным уравнением, имеющим два корня. Обозначим их через К₁ и К₂.      Общее решение уравнения (1) может быть записано в зависимости от величины дискриминанта D=ρ²–4q уравнения (2) следующим образом:      1. При D>0 корни характеристического уравнения вещественные и различные (К₁≠К₂), и общее решение имеет вид  .      2. При D=0 корни характеристического уравнения вещественные и равные (К₁=К₂=К), и общее решение имеет вид:       3. Если D<0, то корни характеристического уравнения комплексные:  , где   – мнимая единица,   и общее решение (К₁=α+βi, К₂=α–βi, β≠0), имеет вид y=e^αx(C₁ cosβx+C₂ sinβx).