20.Вычисление площади поверхности тел вращения.

Пусть гладкая дуга представляет собой график непрерывно дифференцируемой функции . Эта дуга вращается вокруг оси OX, описывая некоторую поверхность. Требуется определить площадь этой поверхности.

Считая элемент поверхности боковой поверхностью усеченного конуса, высотой которого является отрезок , получим . Выделяя здесь линейную часть, пренебрегая квадратичным членом от дифференциала , получаем . Интегрируя и применяя формулу Ньютона – Лейбница, получим

.

Если функция задана параметрически или в полярной системе координат, то в этой формуле производится соответствующая замена переменной, формулы для дифференциала длины дуги приведены выше.

Пример. Дуга графика функции вращается вокруг оси OX, образуя «ведерко». Можно ли налить в это ведерко определенное количество краски так, чтобы окрасить боковую поверхность ведерка?

Во-первых, определим, конечен ли объем ведерка.

, интеграл сходится, объем конечен. Ведерко будет окрашено, если будет окрашена каждая точка поверхности, т.е. в том случае, когда боковая поверхность ведерка будет конечна.

. Так как а интеграл расходится, то по первому признаку сравнения будет расходиться и интеграл . Следовательно, боковая поверхность имеет бесконечную площадь, и боковую поверхность ведерка окрасить не удастся.

21. Вычисление объёма тел вращения.

1. Вычисление объемов тел вращения.

Пусть требуется вычислить объем тела вращения вокруг оси OX.

Тогда .

Аналогично, объем тела вращения вокруг оси OY, если функция задана в виде , можно вычислить по формуле .

Если функция задана в виде и требуется определить объем тела вращения вокруг оси OY, то формулу для вычисления объема можно получить следующим образом.

Переходя к дифференциалу и пренебрегая квадратичными членами, имеем . Интегрируя и применяя формулу Ньютона – Лейбница, имеем .

Пример. Вычислить объем шара .

Пример. Вычислить объем прямого кругового конуса, ограниченного поверхностью и плоскостью .

Вычислим объем, как объем тела вращения, образованного вращением вокруг оси OZ прямоугольного треугольника в плоскости OXZ, катеты которого лежат на оси OZ и прямой z = H , а гипотенуза лежит на прямой .

Выражая x через z, получим .

Искомый объем можно посчитать как разность объемов прямого кругового цилиндра с высотой H и тела, вращения, ограниченного цилиндрической, конической поверхностями и плоскостью OXY

.

21. Задачи, приводящие к дифференциальным уравнениям

Равноускоренное движение. Пусть в начальный момент времени t=0 материальная точка имеет начальное положение S(0)=0, начальную скорость V(0)=V₀ и далее движется прямолинейно с постоянным ускорением a(t)=a. Если S(t) и V(t) – соответственно путь, пройденный точкой за время t, и ее скорость в момент времени t, то S′(t)=V(t) и V′(t)=a(t)=a. Т.е., ф-ция перемещения S(t) явл-ся решением диф.уравнения S′′(t)=a. Найдем решение, интегрируя уравнение дважды.

.

.

2. Уравнение движения. Пусть материальная точка массы m движется прямолинейно под действием переменной силы F(t). Тогда в силу второго закона Ньютона . Поскольку a(t)=S′′(t), то ф-ция перемещения S(t) явл-ся решением диф.уравнения . Это диф. уравнение называют уравнением движения. Например, если рассматривать свободное падение материальной точки в поле тяготения Земли, то действующая на точку сила сводится к силе тяжести F(t)=P=mg и уравнение движения имеет вид S′′(t)=g. Если полагать, что сила сопротивления воздушной среды пропорциональна скорости движения F_c(t)=kV(t), то суммарная сила, действующая на точку, равна F(t)=mg-F_c(t)=mg−kV(t). В этом случае уравнение движения имеет вид . Его решением (для V₀=0) явл-ся ф-ция

Скорость и ускорение такого движения изменяются так

3. Геометрические задачи. Пусть требуется найти линию, проходящую ч/з точку А(1,2) и обладающую следующим св-вом: для любой ее касательной отрезок этой касательной, заключенный м/у осями системы координат, в точке касания делится пополам. Обозначим ч/з y(x) уравнение искомой линии и пусть M(x₀,y₀) - ее произвольная фиксированная точка. Касательная к кривой в этой точке имеет уравнение y-y(x₀)=y’(x₀)(x-x₀). Найдем ординаты точек пересечения этой касательной с осями системы координат.

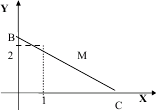
x_B=0, y_C=0. Тогда

Т.к М – середина отрезка BC, то

Отсюда

Т.к. x₀ - произвольная точка, то искомая ф-ция должна удовлетворять диф.уравнению первого порядка

Для произвольной постоянной С ф-ция y(x)=C/x удовлетворяет этому уравнению. Т.к. кривая должна проходить ч/з точку А(1,2), то подставив в это решение x=1 и y=2, получим С=2. Решением явл-ся гипербола y=2/x.