13. Формулы Ньютона-Лейбница.

Формула Ньютона – Лейбница.

Пусть функция непрерывна на отрезке - некоторая первообразная функции . Тогда .

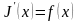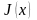Доказательство. Из теоремы о производной интеграла по переменному верхнему пределу следует, что , т.е. - первообразная для функции . По теоремам о первообразных две первообразных отличаются на константу т.е. 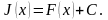Но 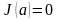(свойство 4 определенного интеграла), поэтому 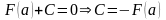. Тогда . Следовательно, .

Формула Ньютона – Лейбница - это одна из немногих формул - связок, связывающих различные разделы математики воедино. Если бы не было формулы Ньютона – Лейбница, то неопределенные интегралы не нашли бы приложения, а определенные интегралы нельзя было бы вычислить аналитически. Именно эта формула делает интегральное исчисление важнейшим инструментом исследования процессов. Любой процесс описывается дифференциальными или интегральными уравнениями, а они решаются в интегралах.

Мы встречались с такими формулами или теоремами – связками. Например, теорема о связи функции, ее предела и бесконечно малой связывает бесконечно малые и пределы. Теорема Ферма и ее следствия – теоремы о средних значениях связывают дифференциальное исчисление и теорию экстремума. В дальнейшем мы тоже будем встречаться с теоремами – связками, они всегда играют фундаментальную роль, например теоремы Остроградского – Гаусса и Стокса в векторном анализе.

13. Замена переменной и интегрирование по частям в определенном интеграле

13. Несобственные интегралы с бесконечными пределами

13. Несобственные интегралы от разрывных функции

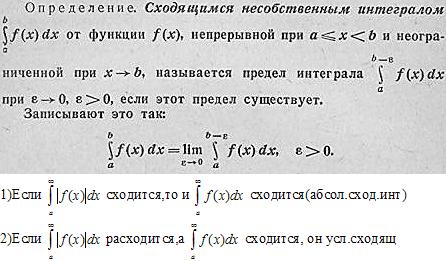
18.Вычисление длины дуги кривой

Для того, чтобы получить формулы для вычисления длины дуги, вспомним выведенные в 1 семестре формулы для дифференциала длины дуги.

Если дуга представляет собой график непрерывно дифференцируемой функции 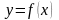, дифференциал длины дуги можно вычислить по формуле

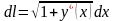. Поэтому

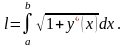
Если гладкая дуга задана параметрически , то

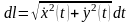. Поэтому .

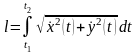Если дуга задана в полярной системе координат, то

. Поэтому .

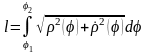Пример. Вычислить длину дуги графика функции , . .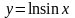

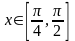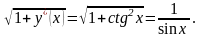
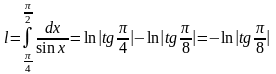Пример. Вычислить длину кардиоиды .

Пример. Вычислить длину одной арки циклоиды. .

.

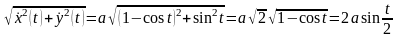
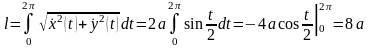19. Вычисление площади плоской фигуры

Вычисление площадей плоских фигур.

1. Фигура ограничена графиком функции, заданной в декартовой системе координат.

Мы пришли к понятию определенного интеграла от задачи о площади криволинейной трапеции (фактически, используя метод интегральных сумм). Если функция принимает только неотрицательные значения, то площадь 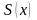под графиком функции на отрезке [a, b] может быть вычислена с помощью определенного интеграла . Заметим, что 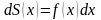поэтому здесь можно увидеть и метод дифференциалов.

Но функция может на некотором отрезке принимать и отрицательные значения, тогда интеграл по этому отрезку будет давать отрицательную площадь, что противоречит определению площади.

Можно вычислять площадь по формуле S=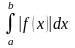 . Это равносильно изменению знака функции в тех областях, в которых она принимает отрицательные значения.

Если надо вычислить площадь фигуры, ограниченной сверху графиком функции , а снизу графиком функции , то можно пользоваться формулой S= , так как .

Пример. Вычислить площадь фигуры, ограниченной прямыми x=0, x=2 и графиками функций y=x², y=x³.

Заметим, что на интервале (0,1) выполнено неравенство x² > x³, а при x >1 выполнено неравенство x³ > x². Поэтому