Интегрирование тригонометрических функций
В зависимости от вида подынтегральной функции можно применять для упрощения тригонометрического выражения различные способы.
Для
интегралов вида
:
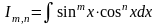а) если хотя бы одно из чисел т,п – нечетное (например, m = 2k + 1), то
.
Пример
9.
б) если т и п – четные, положительные, то степени понижаются сведением к двойному углу по формулам
Пример
10.
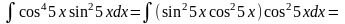
в)
Если т,п
– четные и хотя бы одно из них отрицательно
(или если т
и п
– отрицательные числа одинаковой
четности), то используем соотношения
Пример
11.
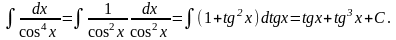
Пример
12.
Интегралы
вида
приводятся
к табличным с помощью формул
Пример
13.
Интегралы
вида
,
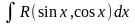где R
– рациональная функция, приводятся к
интегралам от рациональных функций
новой переменной t
в общем случае с помощью подстановки
,
откуда
.
В случае четности R
по sin
x
и
cos
x:
R(-sin
x,
-cos
x)
= R(sin
x,
cos
x)
используем подстановку t
= tg
x,
откуда
.
Пример
14.
При вычислении интеграла применена подстановка .
10. Интегрирование выражений, содержащих положительные степени тригонометрических функций
11. Интегрирование выражений, содержащих отрицательные степени тригонометрических функций
12. Определенный интеграл
Свойства определённого интеграла.
Свойства определенного интеграла.
Свойства линейности
а) суперпозиции
,
б) однородности
Вообще говоря, свойствами линейности обладают все линейные операции (дифференцирование, интегрирование, проектирование и т.д.)
Свойство аддитивности (по множеству)
Доказательство.
Пусть
.
Выберем разбиение так, чтобы точка с
была границей элемента разбиения
.
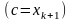Это возможно (следствие). Составим
интегральную сумму
.
Будем измельчать разбиение, сохраняя
точку с границей элемента разбиения.
Это возможно (следствие). Тогда предел
при
левой
части равенства интегральных сумм равен
,
первого слагаемого правой части
,
второго слагаемого правой части
.
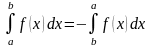(свойство
«ориентируемости» множества).
Составляя интегральную сумму для интеграла в правой части равенства, заметим, что элемент разбиения надо проходить в другом направлении, от конца отрезка к началу. Поэтому для этого интеграла интегральная сумма будет
-
.
Переходя к пределу при измельчении
разбиения, получим
.
.
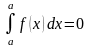Это постулируется, но, вообще говоря,
это и очевидно.
.
.
Если на отрезке
,
то
.
Так как
на отрезке, то
.
Переходя к пределу, получим
.
Если на отрезке
,
то
.
Так как
на отрезке, то
.
Переходя к пределу, получим
.
.
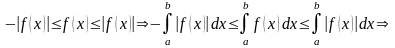(переменная
интегрирования – «немая» переменная,
ее можно изменить, она не несет в себе
самостоятельного смысла)
Определенный интеграл является функцией своих пределов, при фиксированных пределах интегрирования это – число. Он определен своими пределами. Поэтому он и называется определенным.