
- •Первообразная
- •Неопределённый интеграл и его свойства.
- •Правила интегрирования
- •Интегрирование с заменой переменной в определённом интеграле
- •Интегрирование по частям в неопределённом интеграле.
- •Интегрирование выражений, содержащих квадратный трехчлен
- •7. Интегрирование дробно-рациональных функций
- •8. Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •Формулы Ньютона-Лейбница.
- •Вычисление площади плоской фигуры
- •20.Вычисление площади поверхности тел вращения.
- •Вычисление объёма тел вращения.
- •Задачи, приводящие к дифференциальным уравнениям
- •Понятие дифференциального уравнения первого порядка и его решение. Интегральные кривые
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •27. Уравнение Бернули.
- •28. Понятие дифференциального уравнения второго порядка и его решение
- •29. Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •30. Линейные дифференциальные уравнения второго порядка. Свойства их решений
- •31. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •32. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и правой частью специального вида
- •33. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и произвольной правой частью
Интегрирование с заменой переменной в определённом интеграле
Метод замены переменной.
Пусть
1)
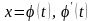 непрерывны при
непрерывны при
 ,
,
значения
 ,
не выходят за границы
,
не выходят за границы
 ,
, ,
,
Тогда

Доказательство.
 .
.
Пример
 .
.

Упражнение. Найдите ошибки в применении теоремы о замене переменной.


Интегрирование по частям в неопределённом интеграле.
Для
вычисления интегралов вида
 ,
если вместо него удобно вычислять
интеграл
,
если вместо него удобно вычислять
интеграл
 ,
пользуются методом интегрирования
по частям.
,
пользуются методом интегрирования
по частям.
=
 -
,
-
,
если интегралы в обеих частях соотношения существуют.
Докажем
справедливость этой формулы. Дифференцируя
произведение функций, получим
 или
или
 .
.
Интегралы левой
и правой частей существуют( ).
).
Интегрируя, получим нужное соотношение.
Примеры.
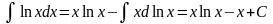
 .
.


Вычислим интегралы
 ,
,
 .
.
 ,
,


 .
.
Теперь, подставляя второй интеграл в первый, получим
 .
.
Аналогично, подставляя первый интеграл во второй, получим
 .
.
Интегрирование выражений, содержащих квадратный трехчлен
7. Интегрирование дробно-рациональных функций
http://www.mathprofi.ru/integraly_ot_drobno_racionalnoj_funkcii.html

Если
рациональная дробь
 является неправильной, то есть
является неправильной, то есть
т ≥ п, то ее можно представить в виде суммы
 где Мт-п
и Rr
– многочлены степеней т-п
≥ 0 и r,
причем r
< n.
Разложение правильной дроби
в сумму простейших имеет вид:
= =
где Мт-п
и Rr
– многочлены степеней т-п
≥ 0 и r,
причем r
< n.
Разложение правильной дроби
в сумму простейших имеет вид:
= =

При этом каждая из простейших дробей, стоящих в правой части равенства, интегрируется в квадратурах.
Таким образом, для того, чтобы проинтегрировать рациональную дробь, необходимо в случае, если она является неправильной, выделить целую часть, затем разложить знаменатель оставшейся правильной дроби на множители степени не выше второй и представить эту дробь в виде суммы простейших дробей, вычислив коэффициенты их числителей с помощью метода неопределенных коэффициентов.
Пример
5.

Подынтегральной функцией является правильная дробь, разложение которой в сумму простейших имеет вид:

Приводя правую часть к общему знаменателю, получаем:

Приравняем коэффициенты при одинаковых степенях х, что приведет к линейной системе относительно A,B,C,D,E:
x4: A + B = 0
x³: -2B + C = 0
x²: 2A + B – 2C + D = 2
x: -2B + C – 2D + E = 2
x0: A – 2C – 2E = 13.
Отсюда A = 1, B = -1, C = -2, D = -3, E = -4. Следовательно,
 ,
где
,
где



 Таким образом,
окончательный результат имеет вид:
Таким образом,
окончательный результат имеет вид:

8. Интегрирование иррациональных функций

После соответствующей замены переменных многие иррациональные функции можно свести либо к рациональным дробям, либо к тригонометрическим выражениям, интегрирование которых будет рассмотрено ниже.
Для
дробно-линейных иррациональностей
удобной заменой является выбор в качестве
новой переменной подкоренного выражения
в степени
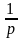 ,
где р
– наименьший общий знаменатель дробных
степеней в подынтегральном выражении.
,
где р
– наименьший общий знаменатель дробных
степеней в подынтегральном выражении.
Пример
6.
 .
.
Сделаем замену переменной: x + 3 = t4. Тогда dx = 4 t³dt. Подставим полученные результаты в подынтегральное выражение:



При интегрировании квадратичных иррациональностей привести подынтегральное выражение к рациональному виду помогают тригонометрические замены:
x
= asin
t,
если в
подынтегральную функцию входит
 ,
,
x
= atg
t
для
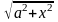 ,
,
 ,
если подынтегральная функция содержит
,
если подынтегральная функция содержит
 .
.
9. Интегрирование тригонометрических функций с помощью универсальной замены
