
- •Первообразная
- •Неопределённый интеграл и его свойства.
- •Правила интегрирования
- •Интегрирование с заменой переменной в определённом интеграле
- •Интегрирование по частям в неопределённом интеграле.
- •Интегрирование выражений, содержащих квадратный трехчлен
- •7. Интегрирование дробно-рациональных функций
- •8. Интегрирование иррациональных функций
- •Интегрирование тригонометрических функций
- •Формулы Ньютона-Лейбница.
- •Вычисление площади плоской фигуры
- •20.Вычисление площади поверхности тел вращения.
- •Вычисление объёма тел вращения.
- •Задачи, приводящие к дифференциальным уравнениям
- •Понятие дифференциального уравнения первого порядка и его решение. Интегральные кривые
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные дифференциальные уравнения
- •27. Уравнение Бернули.
- •28. Понятие дифференциального уравнения второго порядка и его решение
- •29. Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •30. Линейные дифференциальные уравнения второго порядка. Свойства их решений
- •31. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •32. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и правой частью специального вида
- •33. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами и произвольной правой частью
Первообразная
Определение: Первообразной от функции f(x) в данном интеграле называется функция F(x), производная которой равна данной функции:
F’(x) = f(x)
Теорема: Всякая непрерывная функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым.
FxCFxCf x
Определение: Отыскание первообразных называется неопределенным интегрированием, а выражение, охватывающее множество всех первообразных от данной функции f(x) называется неопределенным интегралом от f(x) и обозначается так: ∫f(x)dx.
Свойства:
(∫f(x)dx)' = f(x)
d∫f(x)dx =f(x)dx
∫f’(x)dx = f(x)+C
∫df(x) = f(x)+C
Неопределённый интеграл и его свойства.
Неопределенным
интегралом
 (интеграл от функции
(интеграл от функции
 по
по
 )
называется совокупность всех первообразных
функций для функции
.
)
называется совокупность всех первообразных
функций для функции
.
 .
.
Функция
,
стоящая под знаком интеграла, называется
подинтегральной функцией, а выражение
 - подинтегральным выражением..
- подинтегральным выражением..
Свойства неопределенного интеграла.
Свойства неопределенного интеграла можно условно разделить на две группы. В первую группу собраны свойства, вытекающие из того, что интегрирование – операция, обратная дифференцированию. Во вторую группу собраны свойства линейности. Эти свойства вытекают из того, что интегрирование, как и дифференцирование – линейная операция и определяют линейную операцию.
Первая группа свойств.
 .
.
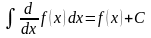

 .
.
Докажем первое свойство.
Так как

Здесь
 -
первообразная для
.
-
первообразная для
.
Докажем второе свойство.
Обозначим
 Тогда
Тогда
 ,
а
,
а
 по первому свойству. Поэтому функции
по первому свойству. Поэтому функции
 являются первообразными для функции
являются первообразными для функции
 .
Следовательно, по теоремам о первообразных,
они различаются на константу, т.е.
.
Следовательно, по теоремам о первообразных,
они различаются на константу, т.е.
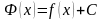 или
или
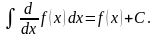
Третье свойство
следует из первого:

Четвертое свойство следует из второго, если вспомнить, что с дифференциалом первого порядка можно обращаться как с алгебраическим выражением (свойство инвариантности формы записи первого дифференциала).
Поэтому надо доказать два первых свойства.
Вторая группа свойств.
свойство суперпозиции
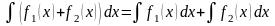
свойство однородности
 .
.
Доказательства того и другого свойств проводятся аналогично. Дифференцируем (по свойствам первой группы) левую и правую часть равенства, приходим к тождеству. Затем из теорем о первообразных заключаем, что левая и правая часть равенства, как первообразные одной и той же функции, различаются на константу. Эта константа может быть формально включена в неопределенный интеграл в левой или правой части равенства.
Для того, чтобы вычислить интеграл от функции, проще всего «угадать» первообразную для этой функции по таблице для производных, переписав эту таблицу в обратном порядке. Запишем интегралы для основных элементарных функций.
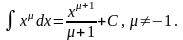
 .
Эти формулы лучше запомнить, они очень
часто встречаются.
.
Эти формулы лучше запомнить, они очень
часто встречаются.


Справедливость этих формул легко проверить, дифференцируя правую часть соотношения и получая подинтегральную функцию.
Правила интегрирования
1.
Вынесение функции из-под знака
дифференциала.
![]() Пример:
Пример:
![]() 2.
Внесение функции под знак дифференциала.
2.
Внесение функции под знак дифференциала.
![]() ,
где
,
где ![]() ,
т.е. является первообразной
,
т.е. является первообразной ![]() .
Пример:
.
Пример:
![]() [
Найдем первообразную функции
[
Найдем первообразную функции ![]()
![]() ]
]
![]() Итог:
Итог: ![]() 3.
Множитель-константу можно выносить за
знак дифференциала и вносить под него
(частный случай первого и второго
правил).
3.
Множитель-константу можно выносить за
знак дифференциала и вносить под него
(частный случай первого и второго
правил).
![]() Пример:
Пример:
![]() .
4.
Под знаком дифференциала можно прибавлять
или отнимать любую константу (частный
случай второго правила).
.
4.
Под знаком дифференциала можно прибавлять
или отнимать любую константу (частный
случай второго правила).
![]() Пример:
Пример:
![]()

